简单即强大：全新生成模型「离散分布网络DDN」是如何做到原理简单，性质独特？

当前，主流的基础生成模型大概有五大类，分别是 ：Energy-Based Models (Diffusion)、GAN、Autoregressive、VAE 和 Flow-Based Models。

本项工作提出了一种全新的生成模型：离散分布网络（Discrete Distribution Networks），简称 DDN。相关论文已发表于 ICLR 2025。

DDN 采用一种简洁且独特的机制来建模目标分布：

1.在单次前向传播中，DDN 会同时生成 K 个输出（而非单一输出）。

2.这些输出共同构成一个包含 K 个等权重（概率均为 1/K）样本点的离散分布，这也是「离散分布网络」名称的由来。

3.训练目标是通过优化样本点的位置，使网络输出的离散分布尽可能逼近训练数据的真实分布。

每一类生成模型都有其独特的性质，DDN 也不例外。本文将重点介绍 DDN 的三个特性：

• 零样本条件生成 (Zero-Shot Conditional Generation, ZSCG)

• 树状结构的一维离散潜变量 (Tree-Structured 1D Discrete Latent)

• 完全的端到端可微分 (Fully End-to-End Differentiable)

• 论文标题： 《Discrete Distribution Networks》

• 论文链接： https://arxiv.org/abs/2401.00036

• 项目链接： https://discrete-distribution-networks.github.io/

• 代码地址： https://github.com/DIYer22/discrete_distribution_networks

离散分布网络原理

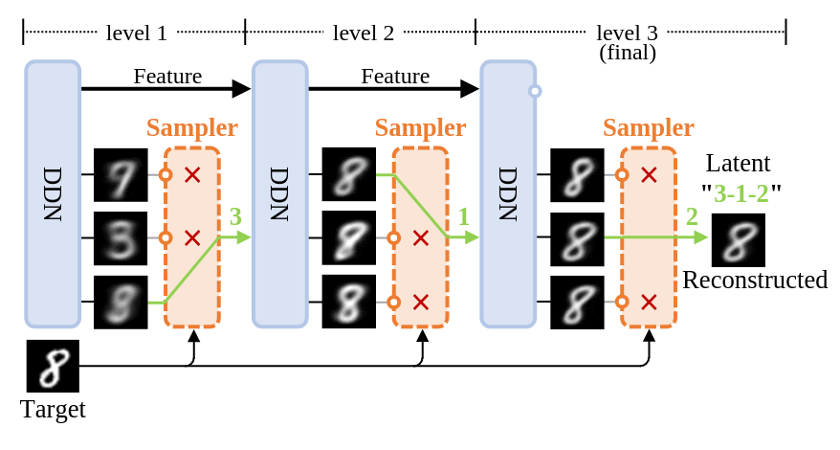
图1: DDN 的重建过程示意图

首先，借助上图所示的 DDN 重建流程作为切入点来一窥其原理。与 diffusion 和 GAN 不同，它们无法重建数据，DDN 能像 VAE 一样具有数据重建能力：先将数据映射为 latent ，再由 latent 生成与原始图像高度相似的重建图像。

上图展示了 DDN 重建 target 并获得其 latent 的过程。一般 DDN 内部包含多个层级结构，其层数为 L，示意图里 L=3。但先让我们把目光集中在最左侧的第一层。

离散分布： 正如上文所言，DDN 的核心思想在于让网络同时生成 K 个输出，从而表示「网络输出了一个离散分布」。因此每一层 DDN 都有 K 个 outputs，即一次性输出 K 张不同的图像，示意图中 K=3。每个 output 都代表了这个离散分布中的一个样本点，每个样本点的概率质量相等，均为 1/K。

层次化生成： 最终目标是让这个离散分布 (K 个 outputs)，和目标分布（训练集）越接近越好，显然，单靠第一层的 K 个 outputs 无法清晰地刻画整个 MNIST 数据集。第一层获得的 K 张图像更像是将 MNIST 聚为 K 类后得到的平均图像。因此，我们引入「层次化生成」设计以获得更加清晰的图像。

接着，从第二层的 outputs 中继续选择出和 target 最相似的一张作为第三层的 condition，并重复上述过程。随着层数增加，生成的图像和 target 会越来越相似，最终完成对 target 的重建。

Latent： 这一路选下来，每一层被选中 output 的 index 就组成了 target 的 latent（图中绿色部分「3-1-2」）。因此 latent 是一个长度为 L, 取值范围 [1,K] 的整数数组。

网络结构

将「重建过程示意图」进一步细化，就有下图 (a) 的网络结构图：

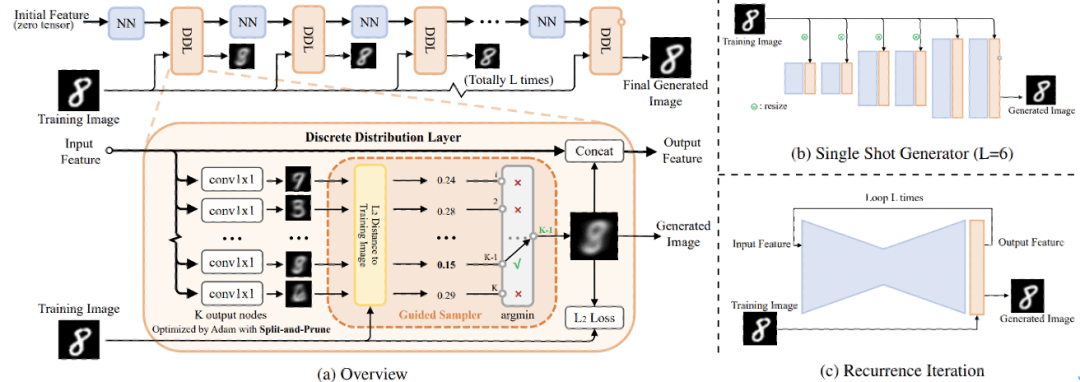
DDN 网络结构示意图和支持的两种网络结构形式

在图 (a) 中，把生成相关的设计整合为 Discrete Distribution Layer (DDL)， 把仅提供基础计算的模块封装为了 NN Block，并重点展示训练时 DDL 内部的数据流。主要关注以下几点：

右侧的 (b)、 (c) 两图分别展示了 DDN 支持的两种网络结构形式:

出于计算效率考虑，DDN 默认采用具有 coarse-to-fine 特性的 single shot generator 形式。

损失函数

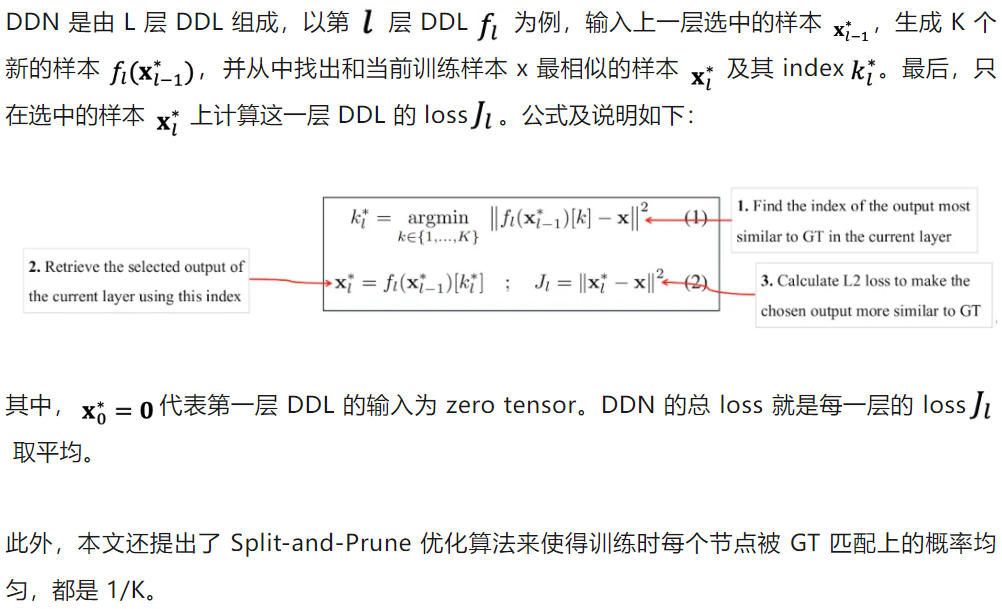
下图展示了 DDN 做二维概率密度估计的优化过程：

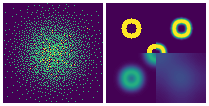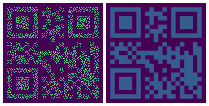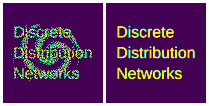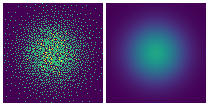
左：生成样本集；右：概率密度GT

实验与特性展示

随机采样效果展示

在人脸数据集上的随机采样效果

更通用的零样本条件生成

先描述一下「零样本条件生成」（Zero-Shot Conditional Generation, ZSCG）这个任务：

• 首先，Unconditional 地训练一个生成模型，即训练阶段，模型只见过图像，没有见过任何 condition 信号。

• 在生成阶段，用户会提供 condition，比如 text prompt、低分辨率图像、黑白图像。

• 任务目标：让已经 unconditional 训练好的生成模型能根据 condition 生成符合对应 condition 的图像。

• 因为在训练阶段，模型没见过任何的 condition 信号，所以叫 Zero-Shot Conditional Generation。

用 Unconditional DDN 做零样本条件生成效果：DDN 能在不需要梯度的情况下，使不同模态的 Condition (比如 text prompt 加 CLIP) 来引导 Unconditional trained DDN 做条件生成。黄色框圈起来部分就是用于参考的 GT。SR 代表超分辨率、ST 代表 Style Transfer。

如上图所示，DDN 支持丰富的零样本条件生成任务，其做法和图 1 中的 DDN 重建过程几乎一样。

具体而言，只需把图 1 中的 target 替换为对应的 condition，并且，把采样逻辑调整为从每一层的多个 outputs 中选出最符合当前 condition 的那一个 output 作为当前层的输出。这样随着层数的增加，生成的 output 越来越符合 condition。整个过程中不需要计算任何梯度，仅靠一个黑盒判别模型就能引导网络做零样本条件生成。DDN 是第一个支持如此特性的生成模型。

换为更专业的术语描述便是：

> DDN 是首个支持用纯粹判别模型引导采样过程的生成模型；

> 某种意义上促进了生成模型和判别模型的大一统。

这也意味着用户能够通过 DDN 高效地对整个分布空间进行筛选和操作。这个性质非常有趣，可玩性很高，个人感觉「零样本条件生成」将会得到广泛的应用。

Conditional Training

训练 conditional DDN 非常简单，只需要把 condition 或者 condition 的特征直接输入网络中，网络便自动学会了 P (X|Y)。

此外，conditional DDN 也可以和 ZSCG 结合以增强生成过程的可控性，下图的第四 / 五列就展示了以其它图像为 ZSCG 引导的情况下 conditional DDN 的生成效果。

Conditional-DDNs 做上色和边缘转 RGB 任务。第四、五列展示了以其它图像为引导的情况下，零样本条件生成的效果，生成的图像会在保证符合 condition 的情况下尽可能靠近 guided 图像的色调。

端到端可微分

DDN 生成的样本对产生该样本的计算图完全可微，使用标准链式法则就能对所有参数做端到端优化。这种梯度全链路畅通的性质，体现在了两个方面：

1.DDN 有个一脉相承的主干 feature，梯度能沿着主干 feature 高效反传。而 diffusion 在传递梯度时，需多次将梯度转换到带噪声的样本空间进行反传。

2.DDN 的采样过程不会阻断梯度，意味着网络中间生成的 outputs 也是完全可微的，不需要近似操作，也不会引入噪声。

理论上，在利用判别模型做 fine-tuning 的场景或着强化学习任务中，使用 DDN 作为生成模型能更高效地 fine-tuning。

独特的一维离散 latent

DDN 天然具有一维的离散 latent。由于每一层 outputs 都 condition on 前面所有的 results，所以其 latent space 是一个树状结构。树的度为 K，层数为 L，每一个叶子节点都对应一个 DDN 的采样结果。

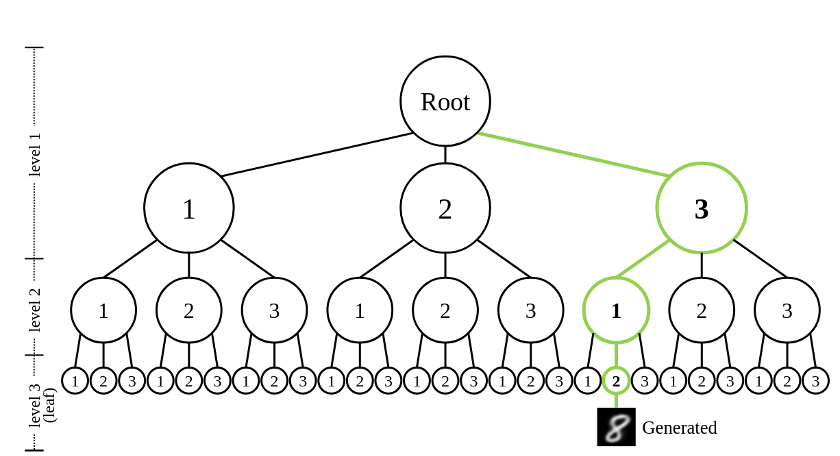
DDN 的 latent 空间为树状结构，绿色路径展示了图 1 中的 target 所对应的 latent

Latent 可视化

为了可视化 latent 的结构，我们在 MNIST 上训练了一个 output level 层数 L=3，每一层 output nodes 数目 K=8 的 DDN，并以递归九宫格的形式来展示其 latent 的树形结构。九宫格的中心格子就是 condition，即上一层被采样到的 output，相邻的 8 个格子都代表基于中心格子为 condition 生成的 8 个新 outputs。

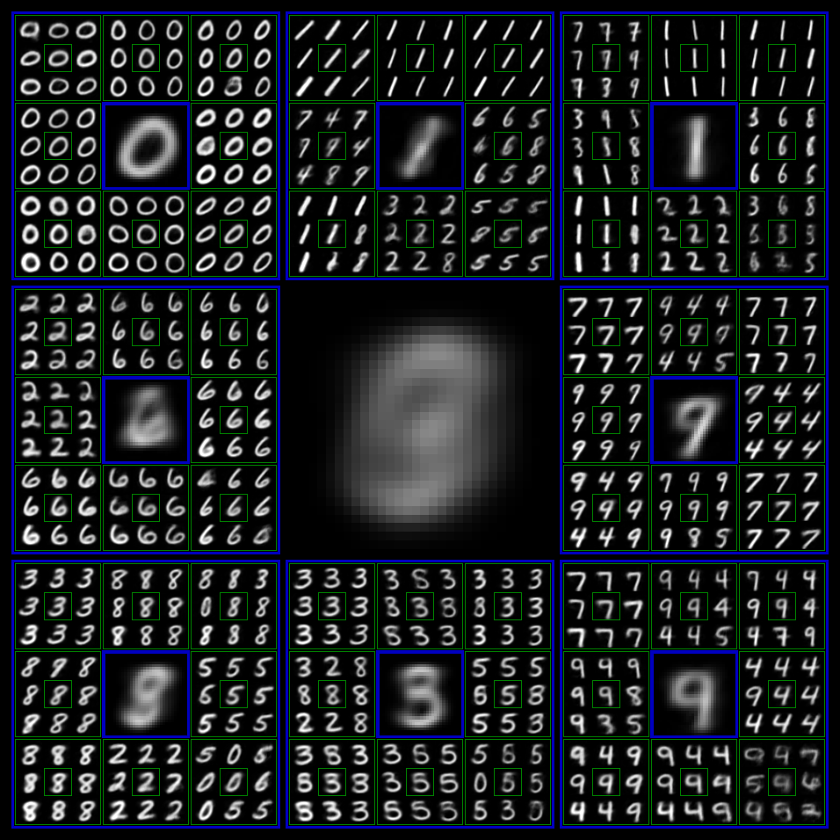
Hierarchical Generation Visualization of DDN

未来可能的研究方向

• 通过调参工作、探索实验、理论分析以改进 DDN 自身，Scaling up 到 ImageNet 级别，打造出能实际使用、以零样本条件生成为特色的生成模型。

• 把 DDN 应用在生成空间不大的领域，例如图像上色、图像去噪。又或者 Robot Learning 领域的 Diffusion Policy。

• 把 DDN 应用在非生成类任务上，比如 DDN 天然支持无监督聚类，或者将其特殊的 latent 应用在数据压缩、相似性检索等领域。

• 用 DDN 的设计思想来改进现有生成模型，或者和其它生成模型相结合，做到优势互补。

• 将 DDN 应用在 LLM 领域，做序列建模任务。

文章来自于微信公众号“机器之心”。