估值840亿AI实验室再放大招，他们要给大模型戴上「紧箍咒」

刚刚，OpenAI前CTO Mira Murati创办的Thinking Machines Lab再次发布成果！

这是他们继《克服LLM推理中的不确定性》（Defeating Nondeterminism in LLM Inference）之后，第二篇研究文章——《模块流形》（Modular Manifolds）。

博客地址：https://thinkingmachines.ai/blog/modular-manifolds/

训练大型神经网络如同「走钢丝」，必须小心翼翼地维持其内部「健康」，防止权重、激活值或梯度这些关键张量变得过大或过小，以免引发数值溢出等一系列问题。

其中一个重要的思路，是为大模型提供一套统一的量级管理。

首先是稳住基本盘。

使用Layer Norm技术把每层的输出拉回合适范围，对激活向量进行归一化（normalization），这也是目前一种普遍的做法。

对梯度更新进行归一化也很常见，例如Muon优化器对更新进行谱归一化处理，使每一步更新的幅度可控。

再进一步，是直接「管住」权重本体。

归一化权重矩阵是一个值得尝试的方向。

文中提出了一种重新思考优化算法提供了新视角：将权重张量约束在某个子流形（submanifold）上，以便与这些流形约束协同设计优化算法。

这好比把「救火」变「预防」：

一开始就把参数放在健康区间，让训练更稳、更具解释性，从而使大模型可以更稳定、高效地训练起来。

流形优化器的形态

我们知道，流形只是一个局部看起来很平坦的曲面。

如果放大到足够多，它看起来就像是一个普通平面。

流形上某一点附近的局部平坦空间称为「切空间」（tangent space）。

如图1所示，三维球面或更高维度的超球面是一个流形，图中以红色部分表示其在某点的切平面。

为了让权重能够「待在」指定的流形里，一个简单的方法是使用普通优化器，在每步更新后将权重投影回流形。

但问题是如果优化步骤偏离流形太多，再被强制投影回来，这会导致名义学习率不再对应参数在流形上的实际位移，从而削弱我们对「步长—效果」关系的直觉。

想在流形上认真设计训练算法，必须先想清楚：在切空间里怎么度量「距离」？

一个解决思路是直接在切空间中进行优化。这样，每一步都是沿着流形「表面」走，学习率能更好地对应「实际位移」。

常见的选择是欧几里得距离，但也可以选择以其他方式测量距离，如图2所示。

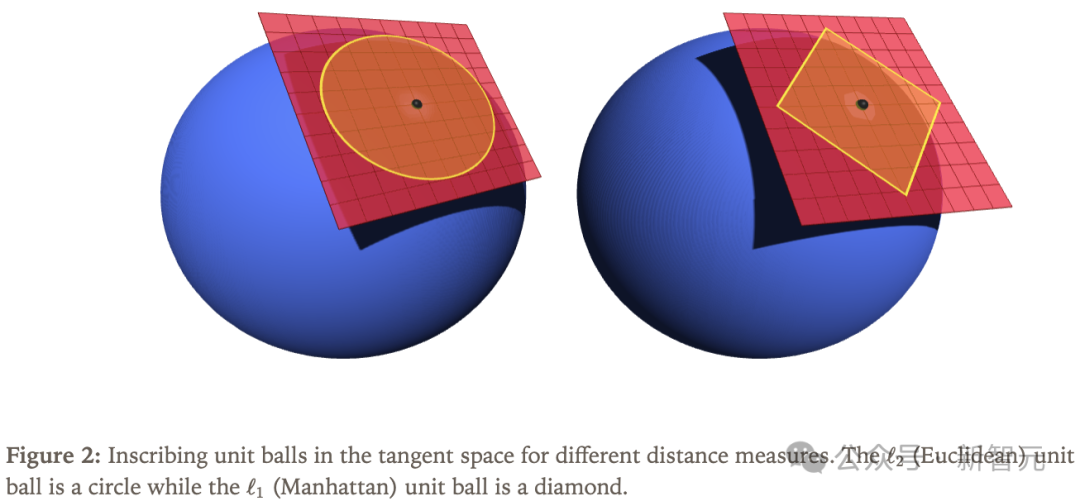
值得注意的是，距离度量方式的选择会直接影响最优优化步骤的方向。

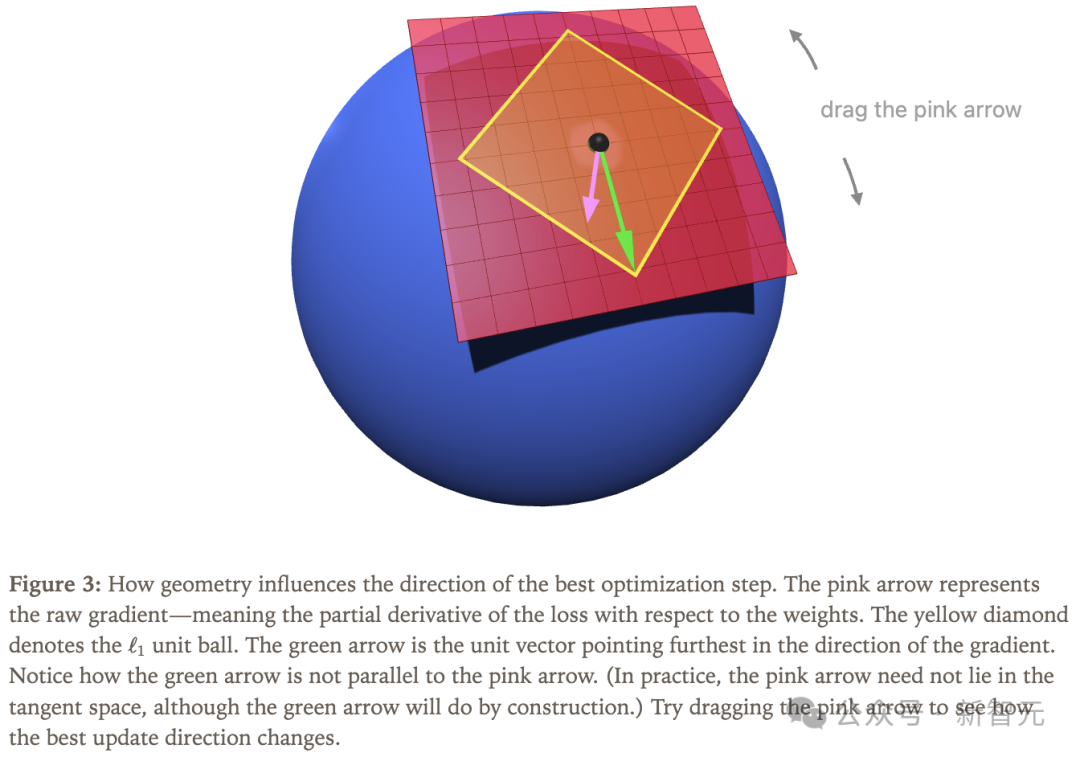
图3中，粉色箭头表示原始梯度——即损失函数对权重的偏导数（partial derivative）。

也就是说，我们不一定非要严格按照梯度方向移动。

为了用数学表达这个过程，我们可以把「在流形约束和特定距离度量下的最优更新方向」看作一个带约束的优化问题，可以用一个搭配欧几里得范数的超球面来举例。

用g表示梯度， w表示超球面上的当前点， a表示更新方向， η表示学习率，我们需要解决的问题是：

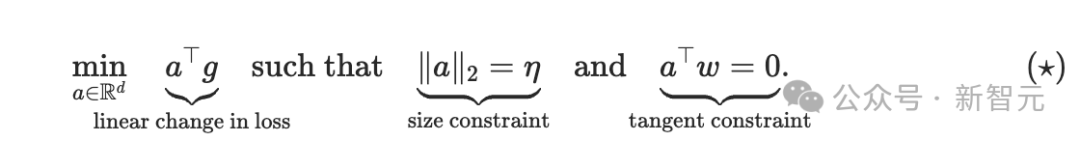
再回到图 1、2 和3所展示的可视化语言，这个公式的意思是：绿色箭头（也就是a的最优解）必须同时满足两个条件：

一是它要落在红色的切平面上，二是它必须在半径为η的黄色圆圈上。

我们可以应用拉格朗日乘数法来求解。

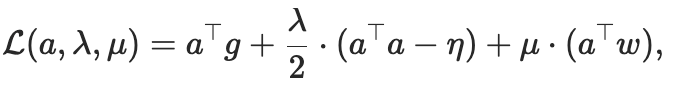
其中λ和μ是拉格朗日乘子。

对这个拉格朗日函数对a求导并令其为零，然后结合两个约束条件求解λ和μ，就可以得到最优更新方向。

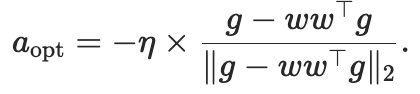
简单来说最优更新的做法是：先从梯度中减去与w同方向的径向分量，即把梯度投影到切空间上，然后将结果归一化，再乘以学习率。

这样得到的更新方向就在切空间里了。

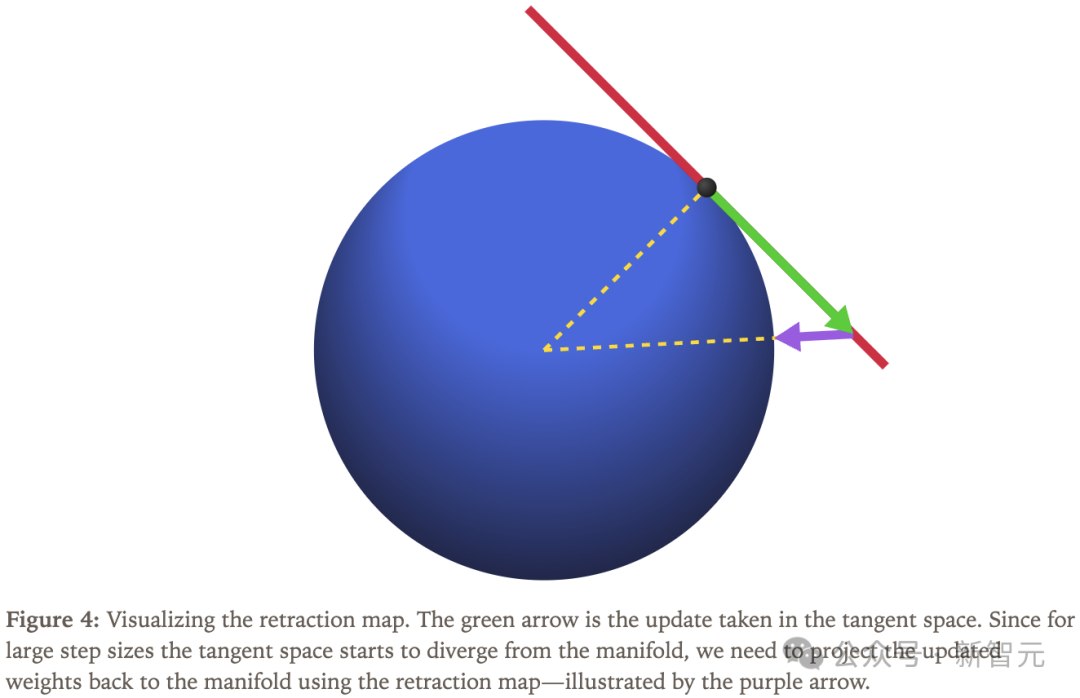
图4中显示这个微小的修正过程被称为「回缩映射」（retraction map）。

完整的流形优化算法如下：

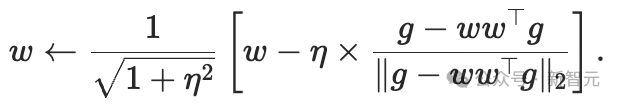
总结来说，一阶流形优化器包含三个步骤：

• 找到一个单位长度的切向量，在梯度方向上尽可能远；
• 用学习率乘以这个方向，然后从当前权重中减去；
• 把更新后的权重通过回缩映射拉回流形上。

在执行这一流程时，我们需要决定选择什么样的流形来作为约束，此外是如何定义「长度」的度量方式。

根据这两个选择的不同，我们就能得到不同的优化算法，具体见下表。

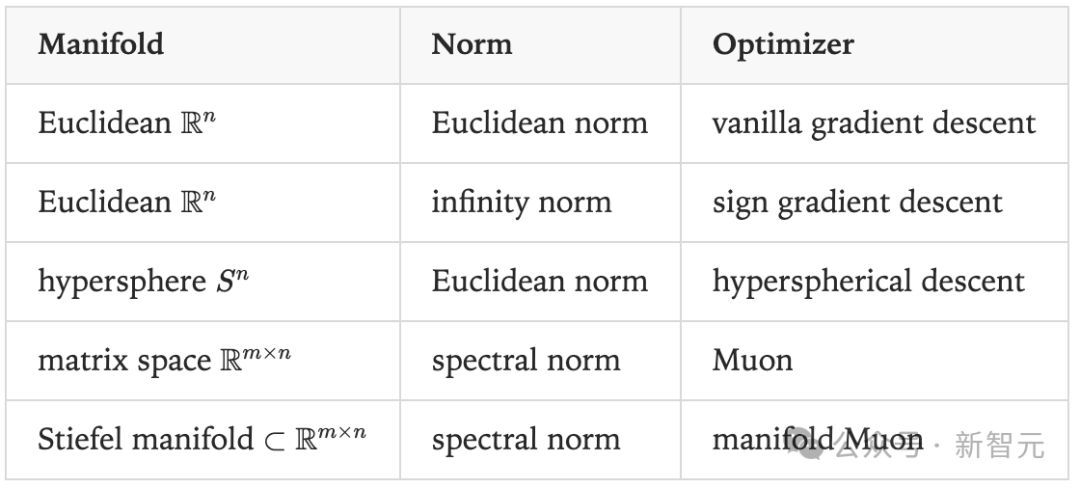
流形Muon

Transformer中的典型权重矩阵W是一个「向量变换器」，即它将输入向量x转换为输出向量y=Wx。

我们希望设计一种流形约束和距离函数，使得该矩阵对输入向量的作用合理：既不应导致输出值过大或过小，也不应在更新权重时引起输出向量剧烈变化或几乎无变化。

一个思考矩阵如何作用于向量的好方法是使用奇异值分解（SVD），如图 5 所示。

SVD以分解矩阵的方式显示矩阵如何沿着不同的轴拉伸输入向量。

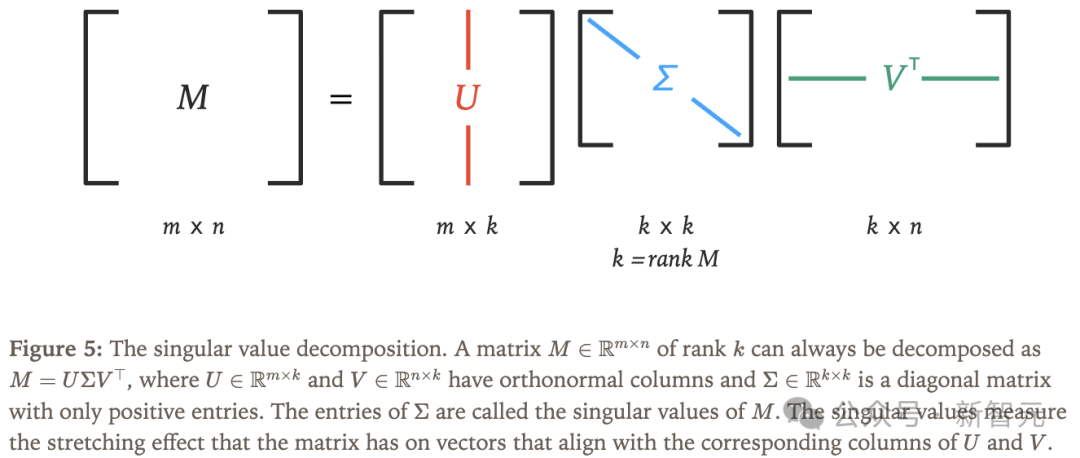
我们希望矩阵的「拉伸效应」接近于1，因此选择了一个所有奇异值均为1的矩阵流形。

这种矩阵流形在数学上被称为Stiefel流形，在高矩阵（ m≥n）的假设下，它可以等价地定义为以下集合：

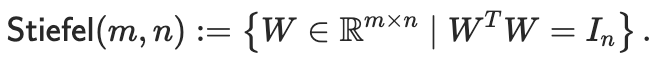
要为Stiefel流形设计优化器，还需选择一个合适的距离函数。

为限制权重更新对输入向量的最大拉伸作用，谱范数（spectral norm），即矩阵最大奇异值的度量是一个合适的选项。

虽然它只约束了最大效应，但由于优化器会饱和这一上限，因此也能间接防止最小效应过小。

正是这一想法，促成了Muon优化器的提出。

这一想法与Stiefel流形约束结合后，就形成了「manifold Muon」问题。

文中的一个关键发现是一个凸优化问题，可以通过标准方法——对偶上升法（dual ascent）来求解。

经过推导，对偶函数的梯度为：

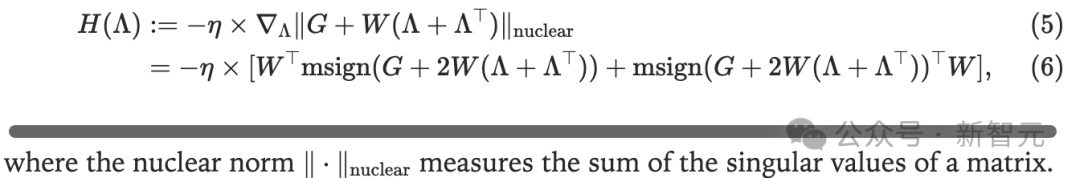
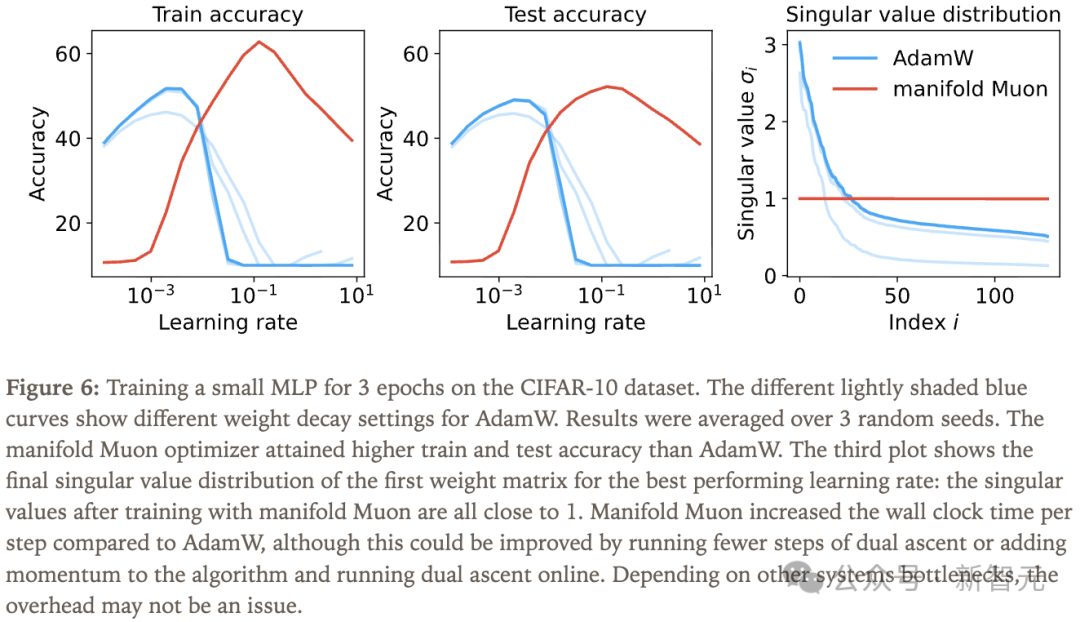
通过一个小实验，可以验证算法的可行性，实验设置与结果见图6。

模块流形

这里还有一个重要的问题：当我们将多个层组合起来构建完整的神经网络时，会发生什么？

是否需要关注层与层之间的交互，并据此修改优化策略？

这需要一种可以将前文介绍的推导逻辑推广到整个神经网络的方法——模块流形（modular manifolds）理论。

该理论的核心思想是：构建一种抽象机制，用来指导如何在各层之间合理分配学习率。

在本质上，在不同层之间分配学习率，或者对单个层进行缩放，都依赖于我们对网络输出对权重的Lipschitz敏感性的理解。

我们在搭建网络的过程中会追踪这种敏感性，而流形约束有助于我们更加精准地把握它。

参考资料：

https://thinkingmachines.ai/blog/modular-manifolds/

文章来自于微信公众号 “新智元”，作者 “新智元”