在大模型的研发中，通常会有下面一些需求：

1.计划训练一个10B的模型，想知道至少需要多大的数据？

2.收集到了1T的数据，想知道能训练一个多大的模型？

3.老板准备1个月后开发布会，给的资源是100张A100，那应该用多少数据训一个多大模型最终效果最好？

4.老板对现在10B的模型不满意，想知道扩大到100B模型的效果能提升到多少？

以上这些问题都可以基于Scaling Law的理论进行回答。本文是阅读了一系列 Scaling Law的文章后的整理和思考，包括Scaling Law的概念和推导以及反Scaling Law的场景，不当之处，欢迎指正。

核心结论

大模型的Scaling Law是OpenAI在2020年提出的概念[1]，具体如下:

1.对于Decoder-only的模型，计算量C(Flops), 模型参数量N，数据大小D(token数)，三者满足: C ≈ 6ND 。(推导见本文最后)

2.模型的最终性能主要与计算量C，模型参数量和数据大小D三者相关，而与模型的具体结构(层数/深度/宽度)基本无关。

固定模型的总参数量，调整层数/深度/宽度，不同模型的性能差距很小，大部分在2%以内

3. 对于计算量C，模型参数量N和数据大小D，当不受其他两个因素制约时，模型性能与每个因素都呈现幂律关系。

4. 为了提升模型性能，模型参数量N和数据大小D需要同步放大，但模型和数据分别放大的比例还存在争议。

5. Scaling Law不仅适用于语言模型，还适用于其他模态以及跨模态的任务[4]：

这里横轴单位为PF-days: 如果每秒钟可进行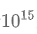次运算，就是1 peta flops，那么一天的运算就是，

这个算力消耗被称为1个petaflop/s-day。

核心公式

第一项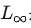 是指无法通过增加模型规模来减少的损失，可以认为是数据自身的熵（例如数据中的噪音）

第二项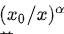是指能通过增加计算量来减少的损失，可以认为是模型拟合的分布与实际分布之间的差。

根据公式，增大X(例如计算量C)，模型整体loss下降，模型性能提升；伴随X趋向于无穷大，模型能拟合数据的真实分布，让第二项逼近0，整体趋向于

大模型中的Scaling Law

GPT4

下图是GPT4报告[5]中的Scaling Law曲线，计算量C和模型性能满足幂律关系

横轴是归一化之后的计算量，假设GPT4的计算量为1。基于10,000倍小的计算规模，就能预测最终GPT4的性能。

纵轴是"Bits for words", 这也是交叉熵的一个单位。在计算交叉熵时，如果使用以 2 为底的对数，交叉熵的单位就是 "bits per word"，与信息论中的比特（bit）概念相符。所以这个值越低，说明模型的性能越好。

Baichuan2

下图是Baichuan2[6]技术报告中的Scaling Law曲线。基于10M到3B的模型在1T数据上训练的性能，可预测出最后7B模型和13B模型在2.6T数据上的性能

MindLLM

下图是MindLLM[7]技术报告中的Scaling Law曲线。基于10M到500M的模型在10B数据上训练的性能，预测出最后3B模型在500B数据上的性能。

Scaling Law实操: 计算效率最优

根据幂律定律，模型的参数固定，无限堆数据并不能无限提升模型的性能，模型最终性能会慢慢趋向一个固定的值

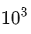
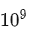
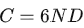
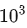
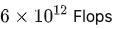
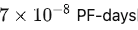
如图所示，如果模型的参数量为（图中紫色的线），在数量达到，模型基本收敛。所以在数据量达到后，继续增加数据产生的计算量，没有同样计算量下提升模型参数量带来的收益大。（计算效率更优）。根据，可以进一步转换成模型参数与计算量的关系，即: 模型参数为，在计算量为，即时基本收敛。也就是右图中紫色线的拐点。

按照上面的思路，下面进行Scaling Law的实操。

首先准备充足的数据（例如1T），设计不同模型参数量的小模型(例如0.001B - 1B)，独立训练每个模型，每个模型都训练到基本收敛（假设数据量充足）。根据训练中不同模型的参数和数据量的组合，收集计算量与模型性能的关系。然后可以进一步获得计算效率最优时，即同样计算量下性能最好的模型规模和数据大小的组合，模型大小与计算量的关系，以及数据大小与计算量的关系。

如图所示，根据左图可以看到计算量与模型性能呈现幂律关系（可以认为数据和模型都不受限制），根据中图和右图，可以发现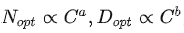，即计算效率最优时，模型的参数与计算量的幂次成线性关系，数据量的大小也与计算量的幂次成线性关系。

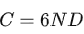
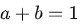
根据，可以推算出，但是a，b分别是多少存在分歧。

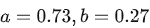
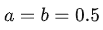
OpenAI[1]认为模型规模更重要，即，而DeepMind在Chinchilla工作[2]和Google在PaLM工作[3]中都验证了 ，即模型和数据同等重要。

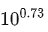
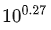
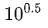
所以假定计算量整体放大10倍，OpenAI认为模型参数更重要，模型应放大 (5.32)倍，数据放大  (1.86)倍；后来DeepMind和Google认为模型参数量与数据同等重要，两者都应该分别放大 (3.16)倍。

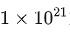
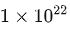
例如在PaLM的实验中，计算量从放大10倍到，模型参数也提升了3.2倍，3.35B->10.7B。

具体最好在自己的数据上做实验来获得你场景下的a和b。

LLaMA: 反Scaling Law的大模型

假设遵循计算效率最优来研发LLM，那么根据Scaling Law，给定模型大小，可以推算出最优的计算量，进一步根据最优计算量就能推算出需要的token数量，然后训练就行。

但是计算效率最优这个观点是针对训练阶段而言的，并不是推理阶段，实际应用中推理阶段效率更实用。

Meta在LLaMA[8]的观点是：给定模型的目标性能，并不需要用最优的计算效率在最快时间训练好模型，而应该在更大规模的数据上，训练一个相对更小模型，这样的模型在推理阶段的成本更低，尽管训练阶段的效率不是最优的（同样的算力其实能获得更优的模型，但是模型尺寸也会更大）。根据Scaling Law，10B模型只需要200B的数据，但是作者发现7B的模型性能在1T的数据后还能继续提升。

所以LLaMA工作的重点是训练一系列语言模型，通过使用更多的数据，让模型在有限推理资源下有最佳的性能。

具体而言，确定模型尺寸后，Scaling Law给到的只是最优的数据量，或者说是一个至少的数据量，实际在训练中观察在各个指标上的性能表现，只要还在继续增长，就可以持续增加训练数据。

计算量、模型和数据大小的关系推导

对于Decoder-only的模型，计算量C(Flops), 模型参数量N(除去Embedding部分), 数据大小D(token数), 三者的关系为: C ≈ 6ND

推导如下，记模型的结构为:

decoder层数: 

attention 隐层维度: 

attention feedforward层维度: 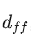， 一般来说 

首先推导模型的参数量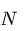（忽略embedding，norm和bias）计算如下:

transformer每层包括: self-attetion 和 MLP 两个部分:

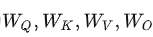
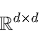
self-attention的参数为，每个矩阵的维度均为，整体参数量：

MLP的层数的参数为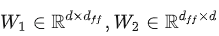，整体参数量:

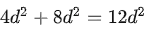
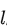
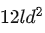
所以每层的参数量为: ，全部的层的参数量为:，即

继续推导模型的前向推理的计算量:

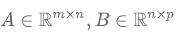
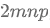
计算量的单位是FLOPs，floating point operations 对于矩阵，，AB相乘的计算量为，一次加法一次乘法。

假设Decoder层的输入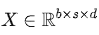，b为batch size，s为序列长度, d为模型维度。

self-attention部分的计算：

输入线性层:

atention计算: 

socre与V的计算: 

输出线性层: 

MLP部分的计算

升维: 

降维:

所以整个decoder层的计算量为:

反向传播计算量是正向的2倍，所以全部的计算量为: 

平均每个token的计算量为

所以对于全部包含D个token的数据集: 

参考资料

[1] Scaling Laws for Neural Language Models

[2] Training Compute-Optimal Large Language Models

[3] PaLM 2 Technical Report

[4] Scaling Laws for Autoregressive Generative Modeling

[5] GPT-4 Technical Report

[6] Baichuan 2: Open Large-scale Language Models

[7] MindLLM: Pre-training Lightweight Large Language Model from Scratch, Evaluations and Domain Applications

[8] LLaMA: Open and Efficient Foundation Language Models

[9] 人工智能中的算力单位Petaflop/s-day - 套牌神仙的文章 - 知乎

[10] 李开复带队零一万物发布开源大模型 Yi，如何解读？ - 黄文灏的回答 - 知乎

[11] 介绍一些Scaling Laws - cingti的文章 - 知乎

[12] 分析transformer模型的参数量、计算量、中间激活、KV cache - 回旋托马斯x的文章 - 知乎

文章来自 “ 知乎 ”，作者 nghuyong 略懂些NLP｜非典型程序员