人类已知最大素数纪录，刚刚被打破！

答案就是——2^136279841-1。

更了不得的是，这个素数是英伟达GPU发现的。

一位「梅森素数猎手」、英伟达前员工，通过自己收集的大量高性能显卡，找到了这个4100万位的最大素数。比起2018年发现的上一个梅森素数，它整整长出1600万位。

这也是史上首个使用GPU找到的梅森素数。

这个素数，终结了个人电脑在发现最大素数上的28年统治。（GIMPS项目之前的所有发现，都是由相对简陋的个人计算机中的CPU完成的。）

所以，发现最大素数，究竟有什么用呢？

帝国理工学院教授数学系教授Kevin Buzzard告诉我们：没有。

是的，这个发现目前完全没有实际应用，但很多数学研究起初都是如此。

现在，最大素数可能没有用，但很可能将来某一天有人会发现它的用途。到那时他们会问数学研究界：「那么，你们的最大素数在哪里？」而数学家们会回答：「其实我们已经研究这个问题几十年了……」

不过，这次做出这一发现的英伟达前员工，还是获得了一点小小的好处——3000美元的奖励。

全新素数霸主诞生

让位吧，2^82589933-1，现在新的素数霸主诞生了。（这个新素数/质数也被称为 M136279841）

英伟达前员工Luke Durant发现的2^136279841-1，比这位多年纪录保持者多出1600万位！

GIMPS激动地表示，这次发现不仅归功于Luke Durant，还要感谢软件开发者和服务器维护者，以及成千上万筛选了数百万非素数的GIMPS志愿者。荣誉属于大家！

为表彰以上所有人员，此次荣誉归于「L. Durant、M. Preda、G. Woltman、A. Blosser等人」

素数是什么？就是只能被1和自身整除的正整数。

这样的数字有2、3、5、7、11……以及^2136279841-1。

2^136279841-1，是由2相乘136279841次，然后减去1得到的。它是已知的第52个梅森素数。

令人着迷的梅森素数

长期以来，素数一直令数学家们着迷。梅森素数是一种形如2^P-1的素数。

最早的梅森素数是3、7、31和127，分别对应P=2、3、5和7。现在已知的梅森素数有52个。

在大约公元前350年，欧几里得首次讨论梅森素数以来，它们一直是数论的核心。

17世纪初，法国修士马林·梅森（Marin Mersenne）提出了一个著名的猜想：哪些P值会产生素数？

为了解决梅森猜想，数学家们花费了300年，还由此诞生了几个重要发现。

有趣的是，梅森的猜想随后被证明不完全正确

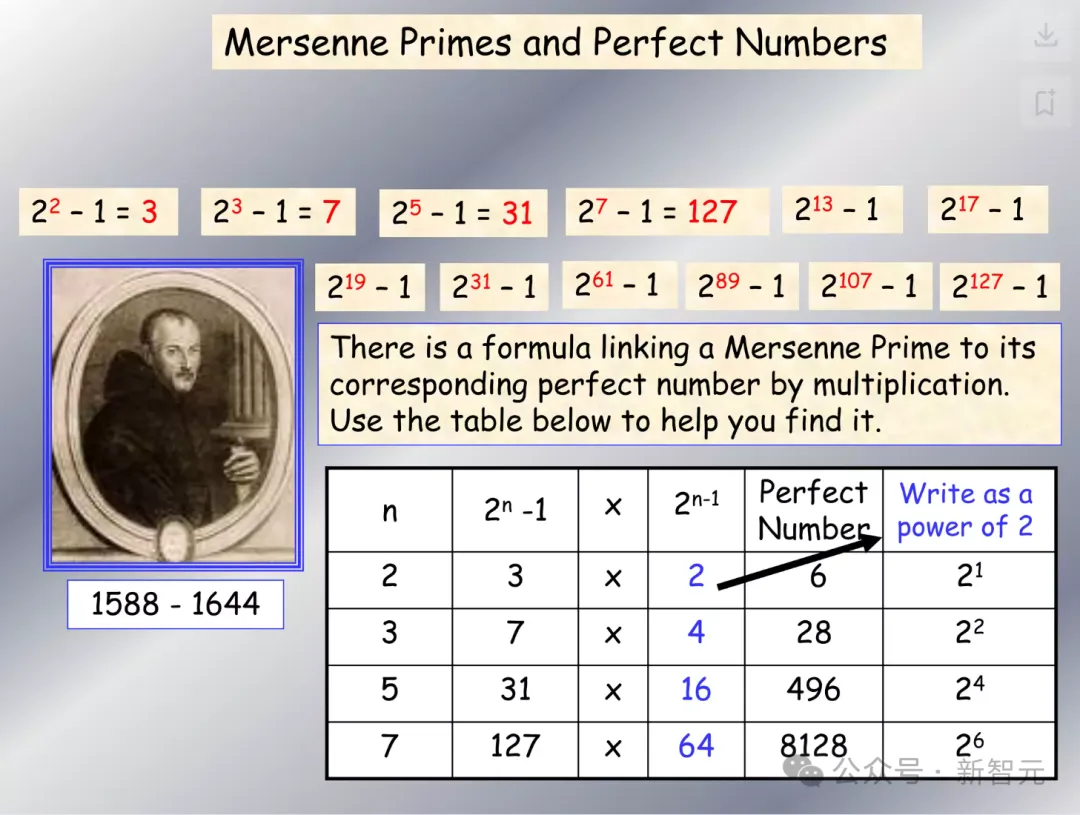
欧几里得证明了每个梅森素数都能生成一个完全数。完全数是其所有真因数之和等于该数本身的数。最小的完全数是6=1+2+3，第二个完全数是28=1+2+4+7+14。

欧拉则证明了所有偶完全数都来自梅森素数。新近发现的完全数是2^136279840 x (^2136279841-1)。这个数字超过了8200万位！

不过，目前尚不清楚是否存在奇完全数。

延续两千年的搜寻

2000多年后，Durant为了寻找这个数字，使用了一台分布在17个国家、由数千个GPU组成的超算。

在爱尔兰的A100计算发现，2^136279841-1很可能是素数；紧接着，在德克萨斯州的H100进行了确认。

寻找梅森素数的项目，叫做梅森素数大搜索（GIMPS，也即Great Internet Mersenne Prime Search）。

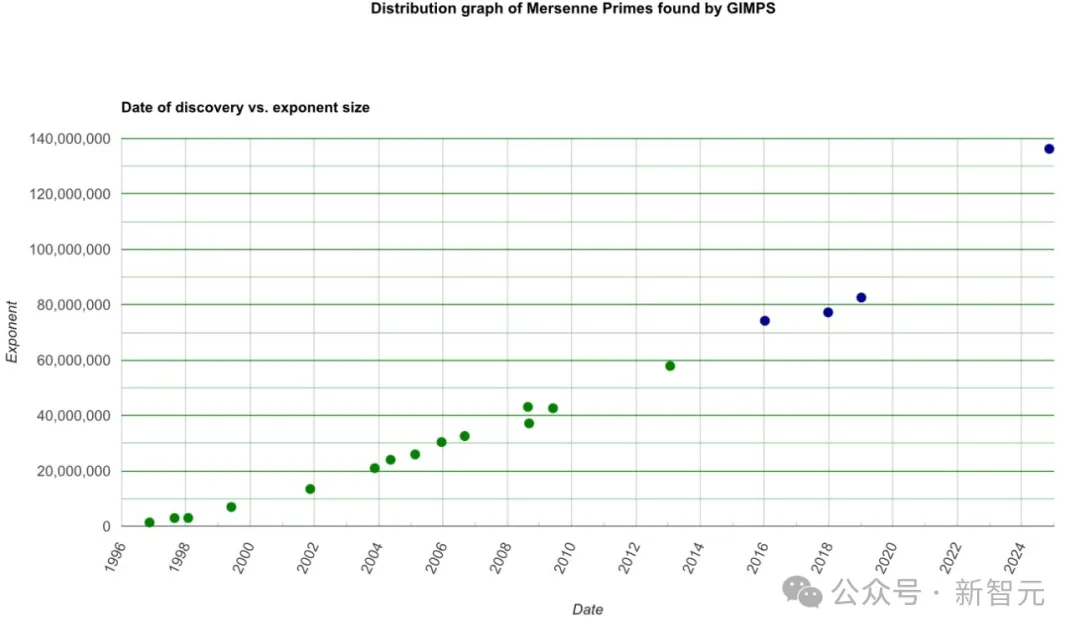
GIMPS成立于1996年，发现了最近的18个梅森素数。

历年发现的梅森素数

这个科研项目背后是一个慈善机构在支持，任何拥有强大的PC或GPU的人，都可以自愿加入成为志愿者——「梅森素数猎人」。

猎人们可以下载一个免费程序来搜索这些素数，任何找到新素数的幸运儿，都将获得3000美元奖励。

GIMPS发现的素数，是用费马可能素数测试来识别的。

然后一旦GIMPS服务器收到可能是素数的通知，就会使用不同程序在不同硬件上运行多个确定性的卢卡斯-莱默素性检验法（Lucas–Lehmer primality test），来进行严格验证。

目前，可能存在尚未发现的较小梅森素数，并且几乎可以肯定，存在等待被发现的更大梅森素数。

就如开头所言，GIMPS在做的事情究竟有什么意义？目前还很难说，因为大梅森素数的实际用途可以说是几乎没有。

这种质疑从几十年前就开始存在，直到后来，人们基于素数开发出了重要的密码算法。

梅森素数猎人们主要是寻找刺激感，因为寻找素数的过程相当于数学和计算机科学的基础研究。这个过程也证明了云超算的能力。

另外，别看这次的3000美元奖励不多，但第一个一亿位数的素数将获得150,000美元的奖金，而到了第一个十亿位数的素数，奖金将升至250,000美元！

各位GPU富人，你们可以行动了。

GPU的崛起

在GIMPS中，36岁的研究员、英伟达前员工Luke Durant，是最活跃的志愿者之一。

此前的猎人们，发现最大素数都是用的CPU。

在2017年，一位叫Mihai Preda的猎人感受到了GPU的巨大潜力，编写了GpuOwl程序用来测试梅森数，并且把软件向所有GIMPS用户开放。

Luke Durant对于GPU的巨大能量一直心知肚明。他认为，如果能找到新的梅森素数，就能证明GPU不仅可以用于AI，也适合于基础数学和科学研究。

从23年10月，Luke开始为GIMPS做贡献，彼时云中GPU可用性的爆炸性增长，为Mihai的软件提供了独特的机会。

于是，Luke干脆开发了一套「云超算」，在多个GPU服务器上运行和维护一套GIMPS软件。

最终，这台云超算跨越了17个国家的24个数据中心，由成千上万个服务器GPU组成。

经过近一年的测试，他成功了！

10月11日，爱尔兰都柏林的一台A100 GPU报告称：2^136279841-1可能为素数。

10月12日，美国德州的一台H100通过Lucas-Lehmer测试，确认了它为素数。

大梅森素数搜索：寿命最长的分布式项目

1996年1月，大梅森素数搜索项目（GIMPS）由George Woltman成立。

1997年，Scott Kurowski使GIMPS能够自动利用数千台普通计算机，来搜索「稀有的数学瑰宝」。

GIMPS是世界上寿命最长的分布式项目之一。

它最初的软件仅在英特尔PC上运行。几年后，Ernst Mayer编写了一个可以在多种非英特尔处理器上运行的程序。这个程序在独立验证几乎每一个GIMPS素数方面，都发挥了重要作用。

十年前，专为GPU设计的软件诞生。几年后，Mihai Preda的突破性gpuowl程序问世。现在，GIMPS可提供适用于各种CPU和GPU的完整程序套件。

GIMPS项目背后的算术算法也有着独特历史。此次发现2^136279841-1的程序，就是基于一种特殊的算法。

1990年代初期，已故的苹果科学家Richard Crandall发现了一种方法，可以将卷积（本质上是大规模乘法运算）的速度提高一倍。

这种方法不仅适用于素数搜索，还适用于其他方面。

为此，Crandall申请了快速椭圆加密系统的专利，利用梅森素数快速加密和解密信息，现由苹果拥有。

George Woltman用汇编语言实现了Crandall的算法，从而产生了一个前所未有高效的素数搜索程序，奠定了所有成功GIMPS项目的基础。

官方答案：为什么要寻找梅森素数？

1. 为了传统！

人们对这于些数学宝藏的追寻，始于公元前300年左右。

当时，欧几里得想要在他的《几何原本》中描述偶完全数。他意识到偶完全数都与某个素数p形式为2ᴾ-1的素数密切相关（现在称为梅森素数）。

随后，Cataldi、笛卡尔、费马、梅森、Frenicle、莱布尼茨、欧拉、Landry、Lucas、Catalan、Sylvester、Cunningham、Pepin、Putnam和Lehmer（仅举几例）依时间先后研究了大素数。

我们怎能不加入这样一个杰出团体呢？

在决定如何处理大数、如何描述其因子以及发现素数的过程中，很多初等数论都得到了发展。

简而言之，探索大素数（尤其是梅森素数）的传统由来已久，硕果累累，值得继承。

2. 探索产生的衍生价值

对美国来说，第一个将人类送上月球具有重大的政治价值，但对社会最具持久价值的是其衍生成果。

比如，为太空探索开发的新技术和材料，如今已成为日常用品；而教育基础设施的改进，让很多人成为了职业科学家和工程师。

寻找下一个创纪录的素数，也是如此。

刚刚提到的那些数学巨匠（如欧几里得、欧拉和费马），都在探索过程中为初等数论留下了伟大的定理（如费马小定理和二次互反律）。

随着时间推移，人们需要找到一种更新、更快的大整数乘法方法。

1968年，Strassen发现了如何使用快速傅里叶变换（Fast Fourier Transform）进行快速乘法运算。1971年，他和Schönhage对方法进行了完善，并成功发表。如今，GIMPS使用的是Richard Crandall开发的改进版算法。

梅森搜索也被教师用来激发学生的研究兴趣。

而这些，仅仅是这项搜索带来的部分衍生成果。

3. 人们喜欢收集珍稀且美丽的物品

梅森素数，通常是已知的最大素数，既珍稀又优美。

自从欧几里得在大约公元前300年开始寻找和研究梅森数以来，发现的还不到50个——这确实称得上珍稀！

同时，它们也很优美。

数学，像所有研究领域一样，有着明确的美学标准。我们寻找那些简短、简洁、清晰的证明，如果可能的话，还要能够将之前不相关的概念结合起来或教会你一些新东西。

梅森素数拥有最简单的素数形式之一：2ⁿ - 1。其素数证明优雅而简洁。

当然，除了这些之外，梅森素数还有一些出人意料的应用。

4. 为了荣耀！

为什么运动员要努力跑得比别人更快，跳得更高，标枪投得更远？仅仅是出于对获胜的渴望。

这种竞争精神并不是为了他人。就如攀岩者被险峻悬崖吸引，登山者渴望山峰。

而梅森素数猎人们，就如同登山者。

他们对人类最大的贡献，并非仅仅体现在实用层面，而是滋养了人类的求知欲望和探索精神。

如果我们失去这种追求卓越的渴望，还能算是真正完整的人吗？

5. 为了测试硬件

自电子计算机时代开始，寻找素数的程序就被用作硬件测试工具。

例如，英特尔会在出货前使用GIMPS项目的软件程序来测试奔腾II和奔腾Pro处理器。而著名的奔腾bug，就是在Thomas Nicely计算孪生素数常数的相关研究中被发现的。

为什么素数程序会被这样使用呢？这是因为它们对CPU和总线要求极高，且程序相对简短，并能够轻易验证答案。在后台运行的同时，亦可进行其他「更重要」的任务。

6. 为了更好地了解分布规律

尽管数学不是一门实验科学，但数学家们经常会寻找具体的例子来验证猜想，并希望能在之后证明它们。

随着研究实例数量的增加，我们对其数学分布的理解也会相应加深。著名的素数定理（Prime Number Theorem）就是数学家们通过仔细研究素数表而发现的。

一些看似简单的计算帮助人们发现了一些有趣模式，比如素数竞赛（Prime Number Races），这些发现催生了大量深入的研究工作。

7. 为了钱？

也有一些人仅仅为了奖金。

毕竟15万美元和20万美元，也是不小的数目了。

参考资料：

https://gizmodo.com/nvidia-computer-finds-largest-known-prime-blows-past-record-by-16-million-digits-2000514948

https://www.mersenne.org/why_join/

https://www.mersenne.org/primes/?press=M136279841

文章来自于微信公众号“新智元”