时隔近70年，那个用来解决最短路径问题的经典算法——Dijkstra，现在有了新突破：

被证明具有普遍最优性（Universal Optimality）。

什么意思？

这就意味着不论它面对多复杂的图结构，即便在最坏情况下都能达到理论上的最优性能！

而且这还是学术界首次将这一概念应用于任何序列算法。

△图源：Quantamagzine

对于Dijkstra算法，想必很多人肯定不会陌生，毕竟它是每个计算机本科生必学的内容。

而且从它诞生至今，已经在广泛地应用于我们的日常生活中，例如在谷歌地图、苹果地图，Dijkstra算法就被用来计算从用户当前位置到目的地的最优路线。

在计算机网络中，被广泛应用于路由协议中；例如开放最短路径优先（OSPF）协议就是基于Dijkstra算法来计算网络中数据包的最优传输路径。

再如通信网络设计、机器人路径规划和物流运输优化等领域，也是处处都有它的身影。

（相关教程可参考：https://www.youtube.com/watch?v=EFg3u_E6eHU）

而这项集结了苏黎世联邦理工、CMU、普林斯顿等顶尖高校科研人员之力的研究，一举让这个经典算法达到了前所未有的高度。

哥伦比亚大学计算机科学家Tim Roughgarden在看完论文后直呼：

这也太神奇了，我无法想象还有比这更吸引人的研究。

据悉，这篇论文已经斩获下周即将举办的理论计算机顶会FOCS 2024（计算机科学基础研讨会）的最佳论文。

一言蔽之，现在的Dijkstra算法，已经被证明是解决单源最短路径问题的“近乎理想”的方法。

那么这项研究又是如何证明和优化的呢？

70年经典算法新突破

首先，我们先通过一个例子，简单回顾一下Dijkstra算法。

如下图所示，Dijkstra算法寻找最短路径的方法，大致可以分为四步：

1.从起点出发：选择起点A。计算从A到邻近点的距离，例如到B的距离为1，到C的距离为5。选择较短的路径，即先前往B。

2.继续探索：从新的点（B）继续查找邻近点的距离，并将这些距离加上从A到B的距离。例如，从A到B的距离是1，B到D的距离是1，因此A到D的总距离为2（1 + 1 = 2）。更新已知的最短路径。

3.记录新的最短路径：在探索过程中发现更短的路径时，更新记录。例如，A到C的原始距离是5，但通过B和D的路径到C的总距离是3（1 + 1 + 1 = 3），比原来的距离短，因此更新A到C的距离为3。

4.重复步骤，直到覆盖所有点：算法继续遍历，直到所有节点的最短路径都被确定。每次优先选择距离最短的路径进行下一步计算，逐步优化到每个点的最短路径。

△图源：Quantamagzine

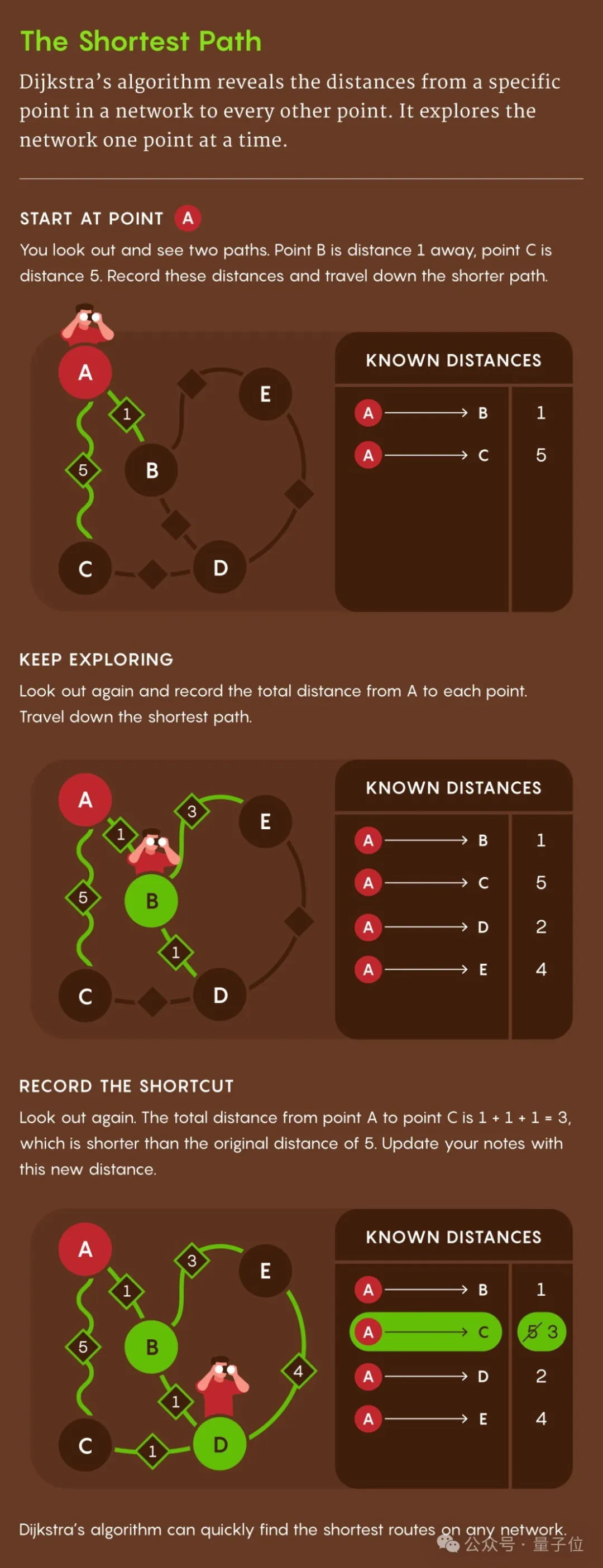
最终，Dijkstra算法可以快速找到网络中从起始点到其他所有节点的最短路径。

在最初的Dijkstra算法论文中使用到了一个简单且关键的数据结构——堆（Heap），而这就为后来的计算机科学家们留下了改进的余地。

例如1984年，两位计算机科学家设计了一种巧妙的堆数据结构，使得Dijkstra算法在解决单源最短路径问题所需的时间上达到了理论极限或“下限”。

从某种特定意义上说，这个版本的Dijkstra算法已经可以说是最好的，也是近40年来的一种“标准”。

而这次的最新论文，研究人员的突破口依旧是这个堆数据结构。

因为他们发现，像Fibonacci堆等常用的数据结构虽然在理论上具有较好的最坏情况时间复杂度（Worst-case time complexity），但在很多情况下未能充分利用图的局部结构特性。

这就导致在处理某些类型的图时，仍然需要高昂的计算代价。

但如果在1984年设计的堆基础上加入对最近插入项快速访问的能力，就可以显著提升算法的效率。

为此，研究人员提出了一种全新的堆数据结构——具备特殊的 “工作集属性”（Working Set Property） 。

所谓 “工作集属性” ，指的是堆能够充分利用操作的局部性，从而优先处理最近插入的元素，降低提取最小元素的成本。

这个概念类似于我们在管理待办事项时，会优先处理那些刚刚添加的紧急任务，从而更高效地完成工作。

若是用公式化的表述，就如下图所示。

对于在堆中插入并随后被提取的任意元素x，其工作集W_x包括了在x被插入后、在x被提取前插入的所有元素，以及x本身。

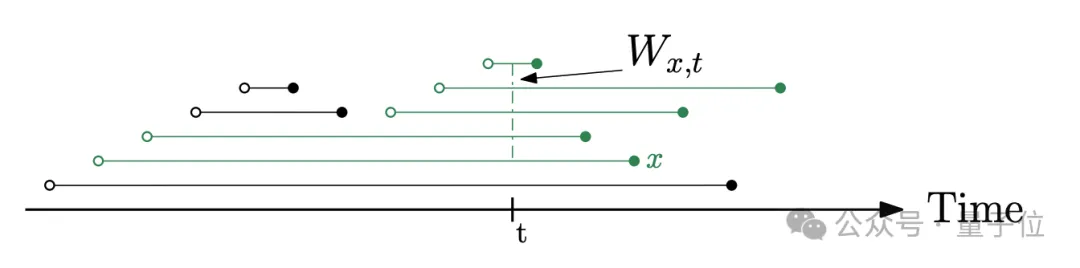
借助这种“工作集属性”，新设计的堆数据结构能够显著提升Dijkstra算法的整体性能，尤其是在具有局部性特征的图上。

也成功使Dijkstra算法具备了普遍最优性，不仅在最坏情况下具有最优性，还能在任何图结构上表现出色。

不仅如此，这项工作还提供了精确的复杂度分析。

例如，作者证明了Dijkstra算法在具有工作集属性的堆上的比较次数是O(OPTQ(G)+n+max⁡_w∈WG∣FG,w∣)。

其中，OPTQ(G)是解决距离排序问题的最优算法所需的比较次数，n是顶点数，∣FG,w∣是前向边的数量。

这也为算法的性能提供了更精确的界限。

总而言之，这些成果不仅推动了图算法的研究，也为实际应用中的算法设计提供了新的视角和工具。

喝咖啡时诞生的算法

关于Dijkstra算法诞生的故事，其实是始于一次意外的灵感。

1956年，年仅26岁的荷兰计算机科学家Edsger Dijkstra当时正试图为一台新型计算机ARMAC编写一个程序，来展示它的计算能力。

有一天，他和未婚妻在阿姆斯特丹购物时走进了一家咖啡馆，正是在休息的片刻中，Dijkstra突然有了灵感，想出了一个计算最短路径的算法。

在没有纸和笔的情况下，他花了大约20分钟在脑海中推演出了这个算法的细节。

正如他在晚年一次采访中所说的那样：

没有纸笔的情况下，你几乎被迫避免所有可以避免的复杂性。

也正是这种简洁和优雅，使得Dijkstra算法在随后的几十年里成为计算机科学领域的经典。

Edsger Dijkstra可以说是一位极具影响力的计算机科学家，他不仅以其最短路径算法闻名，还对计算机科学的许多基础领域做出了开创性的贡献。

Dijkstra出生于1930年，父亲是一位化学家，母亲是一位出色的数学家。

1951 年，Dijkstra在父亲的建议下前往剑桥参加了一门为期三周的编程课程，这次经历改变了他的职业轨迹。

在此期间，他遇到了著名的数学家和计算机科学家Adriaan van Wijngaarden，并由此获得了在阿姆斯特丹数学中心（Mathematical Centre）的工作机会。

Dijkstra是荷兰首位以“程序员”身份被雇佣的人，1956年完成学业后，他继续在数学中心工作，并于1959年发表了他的著名论文A Note on Two Problems in Connexion with Graphs。

这篇论文介绍了他提出的最短路径算法，后来成为了计算机科学中引用次数最多的论文之一。

尽管Dijkstra的算法十分优雅，但当时几乎没有计算机科学期刊，发表过程十分困难，最终他选择将其发表于新创刊Numerische Mathematik上。

Dijkstra在职业生涯中赢得了极高的声誉，并于1972年获得计算机科学领域最负盛名的图灵奖。

他不仅在编程语言、操作系统和并发控制等领域做出了许多基础性贡献，还以其对编程方法学的深入思考而著称。

他强调程序的正确性，认为程序应该从一开始就正确地设计，而不是通过调试来达到正确。

不过与此同时，Dijkstra的性格也非常独特，他既被赞赏也被批评，是一位充满争议的人物。

他对于计算机科学的教育和研究有着强烈的观点，常常发表极具挑战性的言论。

例如，他反对使用goto语句，并在1968年发表了著名的文章Go To Statement Considered Harmful，这篇文章引发了广泛的争议，但最终他的观点得到了普遍认可。

Dijkstra算法不仅可以计算从起始点到一个目的地的最短路径，还可以给出从起始点到所有其他节点的排序，这正是单源最短路径问题的解决方案。

它的核心思想是不断探索当前距离最短的路径，更新每个节点的最短距离，直到所有节点的距离都确定下来。

这种算法的简洁性和高效性使得它成为经典的路径规划工具。

麻省理工学院的计算机科学家Erik Demaine曾评论道：

这是一个伟大的算法，速度非常快，简单易实现。

但算法的成功不仅归功于其核心思想，还离不开数据结构的选择，在几十年的发展中，研究人员不断改进堆数据结构，使得算法的整体性能不断提升。

而这一次，改良堆数据结构，可以说是再次立功了。

论文地址：

https://arxiv.org/abs/2311.11793

参考链接：

[1]https://www.quantamagazine.org/computer-scientists-establish-the-best-way-to-traverse-a-graph-20241025/

[2]https://inference-review.com/article/the-man-who-carried-computer-science-on-his-shoulders

文章来自于微信公众号“量子位”，作者“金磊”