国际奥数题手到擒来,OpenAI o1是靠死记硬背还是真的实力超群?
近日,来自港大的研究人员对o1进行了严格的AB测试:

论文地址:https://arxiv.org/pdf/2411.06198
如何判断LLM是否真正具有强大的数学推理能力?
考两张卷子:一张是有可能提前背题的,另一张是不太可能提前背题的,两张卷子难度一致。
如果LLM两次考试的分数差不多,就证明人家是真会;要是后者的成绩明显低于前者,那就有作弊嫌疑了。
本文中,OpenAI Orion-1模型面对的两张试卷,分别取自国际数学奥林匹克(IMO)和中国国家队训练营(CNT)的试题。
IMO的题目很容易获得,而CNT的题目则无法公开访问,通过比较o1模型在两个数据集之间的性能,作者得出结论:o1是真有实力!
OpenAI o1的亮相直接掀起了推理模型的风潮。
o1采用强化学习来训练token-wise奖励模型,模拟了推理和反思过程,从而在token生成中培养了一种内在的思维链风格。
从本质上讲,o1的推理是一个制定和执行计划的过程。
OpenAI曾表示,o1-mini在美国高中AIME数学竞赛中的分数可以排进全美前500,但也有一些评测表示o1的效果并不理想。
为了公平测试o1的数学推理能力,本文的研究者编译了两个数据集进行分析。
第一个数据集包含来自过去十年国际数学奥林匹克竞赛(IMO)的60个问题;第二个数据集包含来自中国国家队(CNT)训练营的60个问题(非公开)。
注:CNT训练营旨在为学生在中国的IMO比赛做好准备。中国国家队的选拔过程涉及多次测试(通常为8-10次),每次持续4个半小时,与实际IMO比赛的形式相同。
针对测试事先作出假设:
原假设:o1-mini的问题解决能力是基于推理能力的;
备择假设:o1-mini的性能可能来源于对问题和解决方案的记忆,或对预训练模式的模仿。
对于原假设,可以预计模型在IMO和CNT数据集中表现出类似的性能水平。相反,在备择假设下,o1在两个数据集之间将存在显著的性能差异(IMO数据集的得分更高)。
另外,原假设还表明o1-mini能够将其推理技能推广到不同的问题集中,而不管它们的来源或复杂性如何。
latex是编写数学问题和编辑软件的标准格式,这里将三个数据集从PDF转换为latex文件,以便o1可以轻松读取和处理。
o1不需要CoT这种额外的提示,实验中直接将latex问题文件提供给 o1-mini模型。
评测采用IMO或CNT数学竞赛中采用的标准评分方法:每道题最多7分;当问题需要数字答案时,提供正确的数字将获得1分;如果解决问题的直观方法是正确的,则获得2分;其余4分保留用于展示细致准确的推理步骤。
在严格数学领域,推理的复杂性和逻辑步骤的精确性非常重要,而LLM所擅长的整体概念理解在评分过程中受到的重视相对较低。
对于以证明为导向的问题,评分系统将2分分配给基本正确的思维链(表明解决方案的逻辑路径);其余5分取决于LLM能否给出详细而严格的论点,强调数学证明中连贯推理的必要性。
在评估o1-mini的响应时,作者观察到模型难以始终如一地提供严格的证明步骤。
与正式证明相比,o1-mini通常表现出「试错法」:进行了一系列尝试,偶尔通过非正式推理和启发式猜测得出正确答案,这种非正式的推理缺乏数学证明所期望的严谨性和正式性。
下图展示了一个例子,o1-mini通过验证一些只涉及小自然数的情况来「猜测」答案。

基于o1-mini的这种特性,下面就不再要求正式的证明,而侧重于评估模型展示正确直觉并通过推理得出正确结果的能力。
新的评价标准根据性质将问题分为两种不同的类型:
1. 搜索类型:这类问题需要找到特定类型的数字、整数或基于表达式的解决方案,比如下面这个例子:

2. 解决类型:这类问题涉及寻找方程或优化问题的解决方案。
评分过程由精通相关数学领域的人工评估员负责。所有问题集、等级和相应的标签都可应要求进行审查,从而确保评估结果的透明度和可访问性。
下表展示了两个数据集(IMO和CNT)上不同类型问题的分布情况。
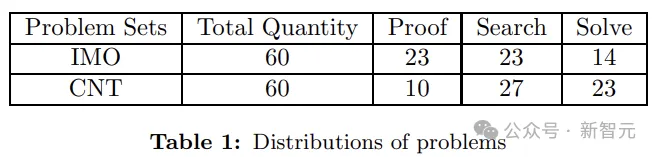
实验的关键评估指标是,检查o1-mini能否在Search和Solve类型的问题中提供正确的答案,结果如表2中所示。

第一列展示了o1-mini在搜索类型问题上的实际准确率(包括23个IMO问题和27个CNT问题),最后一行统计量t的计算公式如下:
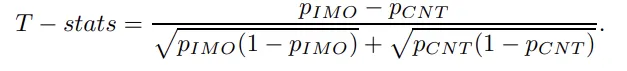
对于「Search」和「Solve」类型的问题,统计量t都非常接近0,这表明公共数据集(IMO)和私有数据集(CNT)之间,o1-mini模型的性能没有统计学上的显著差异。
也就是说,o1-mini的能力不是来自简单地记住解决方案,而是源于其推理能力。
o1通常以叙述风格编写的思维过程和以数学严谨的语言编写的最终解决方案。
在某些情况下,思考过程中提供的直觉可能是关键的一步。此外,在最终解决方案部分突出的逻辑错误也很普遍,例如在回答搜索类型的问题时未能论证其他解决方案不存在。

第一个例子题目如上图所示,两人轮流占位,对Amy的额外要求是两点之间的距离不能等于√5,求Amy最多能占多少个位置。
首先,o1-mini分析了√5的限制(即两点的坐标差为(1,2)或(2,1)),可以等效成下图黑白点的站位,此时相同颜色的点距离都不会等于√5。
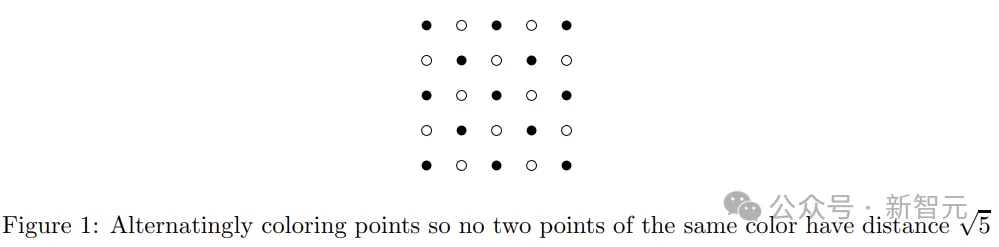
于是,O1-mini得出结论,Amy应该将她的石头放在相同颜色的点上。
在这个例子中,o1-mini提供了有用的直觉,并给出了正确答案,但 模型也没有解释为什么Amy不能占更多的点。

对于上图的问题,o1-mini测试了从1到18的整数,然后选择了几个较大的数字。通过分析满足条件的数字,它发现了只有质数的幂才可行的模式。
然后,o1-mini正确地证明了为什么质数的幂通常是可行的。然而,对于其他合数,o1-mini只提供了一些例子来说明。
在这个问题中,o1-mini坚持测试小的、易于计算的案例,这种方法在大多数搜索类型的问题中很常用,而且一般能拿到大部分分数。
下一个问题,找出所有符合条件的实数:

对此,人类的推理过程一般首先考虑α是整数的情况,然后分别评估奇数和偶数两个子情况,可以使用求和公式写出结果并进行推断。
实验中,o1-mini以类似的方式开始,几乎完美地复制人工解的步骤。对比细节可以发现模型的推理存在疏忽,比如没有考虑整数分量的奇偶校验(奇偶性不会影响实际答案)。

最后一个例子的推理稍微复杂一些,o1-mini终于做错了。它这次选择了暴力破解:遍历每一列,直到找到怪物或到达最后一行。
虽然o1-mini正确识别出有一个安全的列,但它没有认识到探索怪物下方以到达最后一行的重要性。
这表明o1-mini缺乏强大的空间推理能力(即使是在二维空间中),并且与人类相比缺乏解决问题的策略。它无法解决问题可能是由于缺乏公式化的分步方法,或是用来确定最有效算法的规则。
参考资料:
https://arxiv.org/abs/2411.06198
文章来自于微信公众号“新智元”
