陶哲轩震撼！数学家1975年埋下的「坑」，被AI和全球网友用48小时填平了

刚刚，AI又破解了一个数学难题！

Erdos#1026问题已经被攻克，且给出了正式证明。

而在此之前，这个问题已经困扰了数学界50年。

陶哲轩在Mastodon上宣布了这一消息，还在一篇博客中详细讲述了这个故事。

他强调，在AI的辅助下，人类团队仅用了48小时，就顺利攻克了这一难题。

并且，AI在此过程中带来的是全新理解，绝非搜索这么简单。

要知道，如果是靠传统方法，只靠数学家使用编程和文献检索，可能会需要数周甚至数月。

在这个过程中，AI实际上是在生成新的数学洞见，而不仅仅是检索现有文献。

Harmonic官网也宣布了这一消息，其AI系统Aristotle参与了此次解题过程。

Erdos#1026问题

1975年，传奇数学家保罗·埃尔德什在一篇论文的角落随手写下一个问题。

半个世纪后，这个问题静静躺在「埃尔德什问题网站」上，编号1026。

谁也没想到，它会在2025年的最后一个月，被一群数学家利用AI工具，在短短48小时内彻底破解。

埃尔德什的原问题，读起来有点像谜语。

给定一串不同的实数x1,x2,…,xn，定义S(x1,…,xn)为所有单调子序列（递增或递减）的最大可能和。

这个函数有什么性质？

问题一出，大家面面相觑：这到底要问什么？是求S的表达式？还是找它和总和的比值下界？

2025年9月12日，问题被挂上网站时，附加了一条注释：「该问题表述较为模糊。」

但数学家的本能，就是要把模糊变成精确。

当天，网友Desmond Weisenberg提出了一个清晰的游戏化解释：

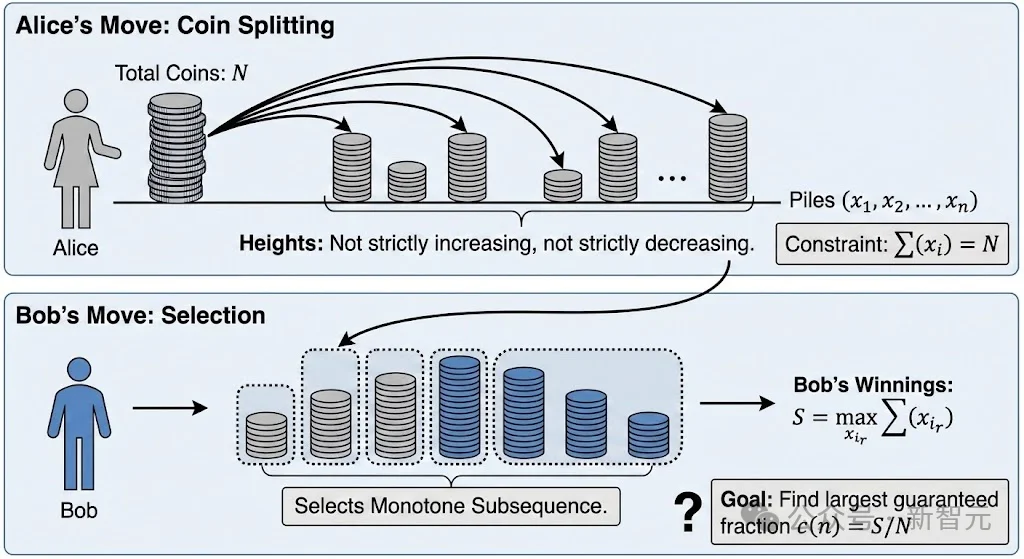
Alice和Bob的硬币游戏

Alice有N枚硬币，她分成n堆，每堆xi枚（xi可不同）。Bob可以选取一个单调的子序列（递增或递减），拿走这些堆里所有硬币。

问：无论Alice怎么分堆，Bob至少能拿到总硬币数的多少比例？

这个比例，记作c(n)。

从n=3到平方数猜想

可以先看这样几个例子。

很快，Stijn Cambie发现：

如果Alice把硬币分成k2堆，每堆差不多大，并排列成k个递减块，每块k 堆，块之间递增，那么最长单调子序列只有k堆。

于是Bob最多拿到1/k的比例，也即c(k2)≤1/k。

反过来，Wouter van Doorn用已有结果给出下限：c(n)≥(1/√2)/√n。

那么，√n·c(n)的极限是多少？它在1/√2和1之间。

第二天，Stijn手算小n的值：

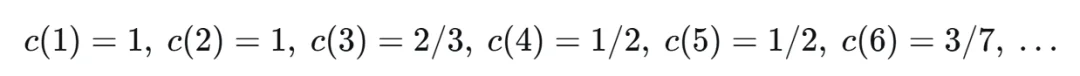
数据虽少，但已足够让他大胆猜想：c(k2)=1/k。

这意味着√n·c(n)→1，Bob在n很大时几乎能保证拿到约1/√n的比例。

AI出手了！

两个月后，2025年12月7日，Boris Alexeev用AI工具Aristotle在证明辅助语言Lean中自动证出了c(k2)=1/k。

几乎同时，Koishi Chan给出一个优美的人类证明——「膨胀法」。

至此，上下界合一，猜想成功得证。

更巧的是，这个答案，其实早就存在了。

Google Scholar很快找到一篇2016年论文，其中已有此结果，并引用了更早的Wagner用「膨胀法」处理埃尔德什-塞凯赖斯定理的工作。

原来，数学早已悄悄解决过这个问题，只是未被链接到埃尔德什的原始提问。

AI登场

猜出完整公式

但故事的高潮还在后面。

陶哲轩决定用另一个AI工具AlphaEvolve系统探索c(n)。

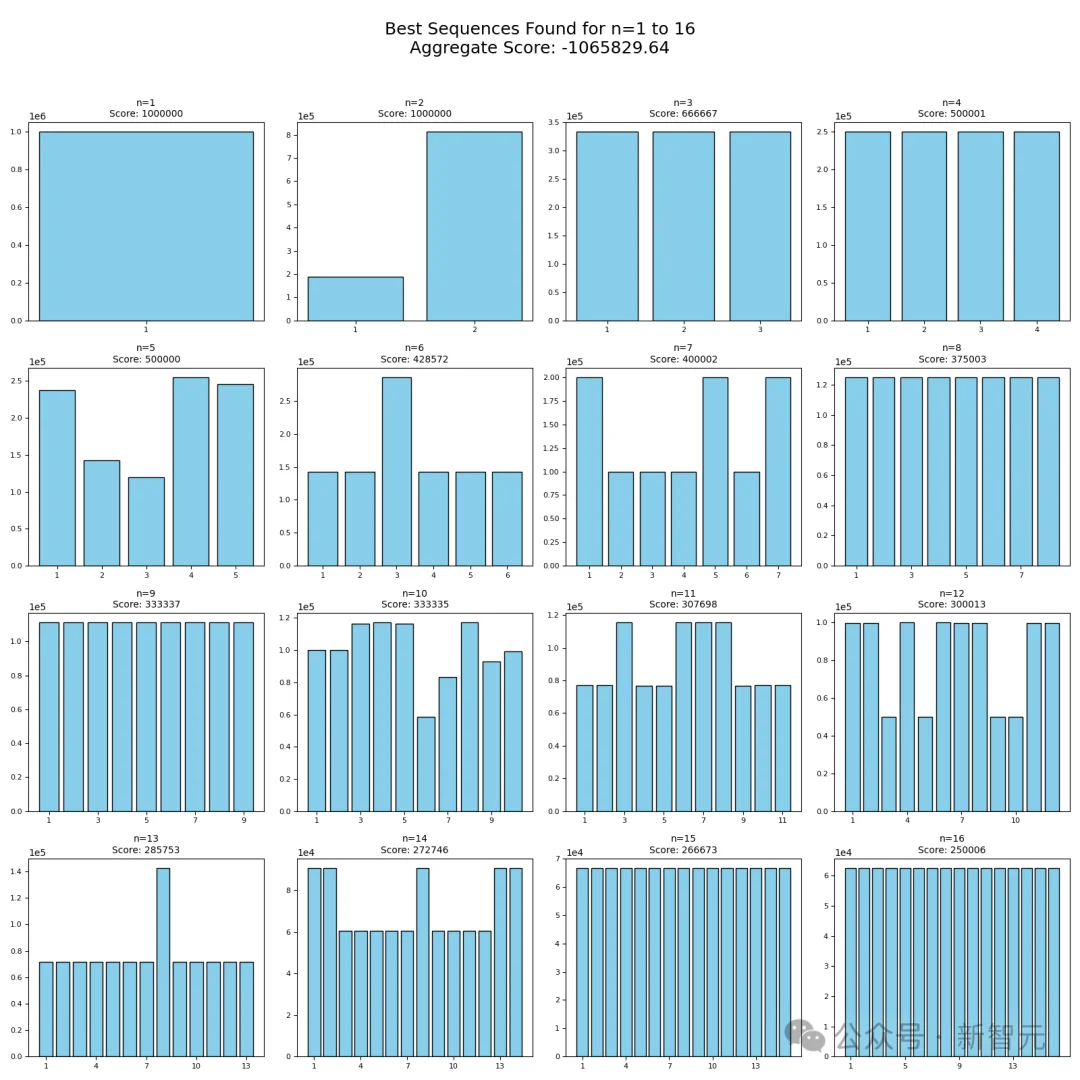
他让AI尝试构造使S尽量小的序列，很快得到n=1到16的数值结果：

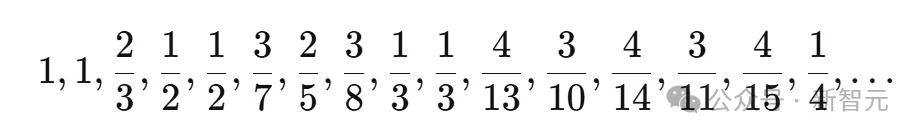
这些分数看似杂乱，但重新排列后，模式逐渐浮现了出来。

Boris从中提炼出干净公式：

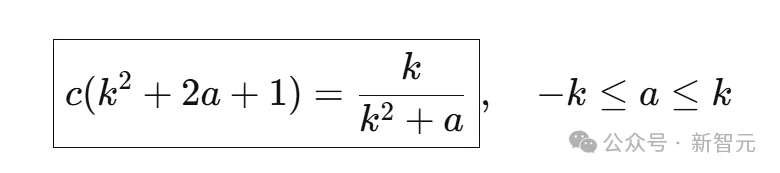
并构造出极值序列：用「红」「蓝」两种数值的块交替排列，控制单调子序列的长度。

下图直观展示了该构造（a≥0的情形）：

而1/c(n)的图像，正是对√n的分段线性逼近：

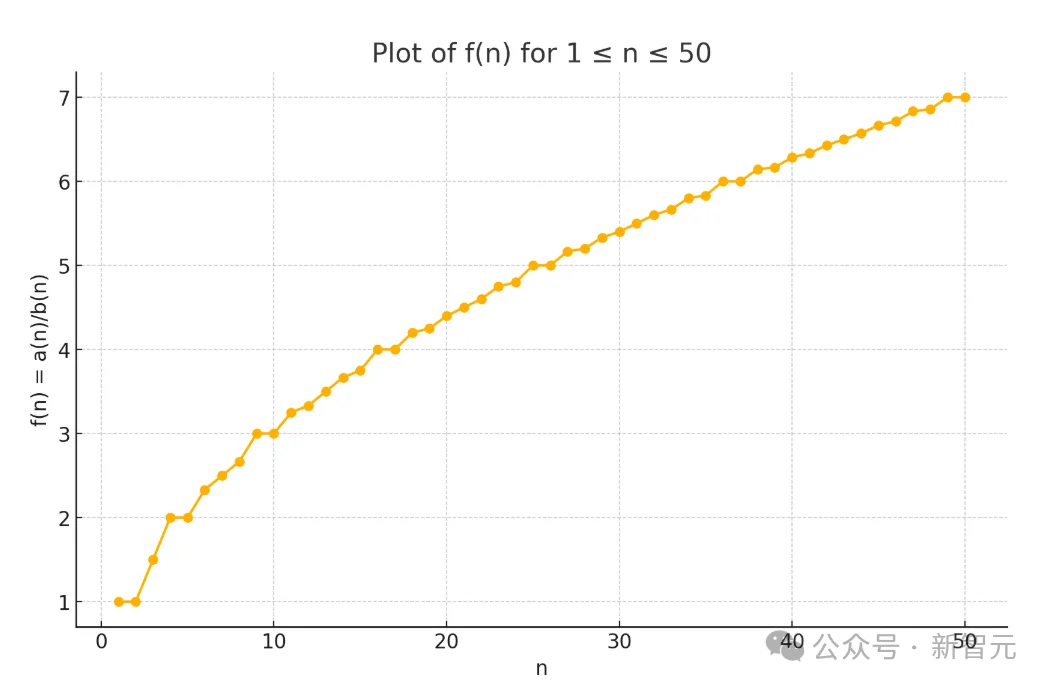
连接经典

正方形填充问题

随后，Lawrence Wu指出：此问题等价于一个正方形填充问题（埃尔德什问题106）。

Lawrence证明：c(n)≥1/f(n)。

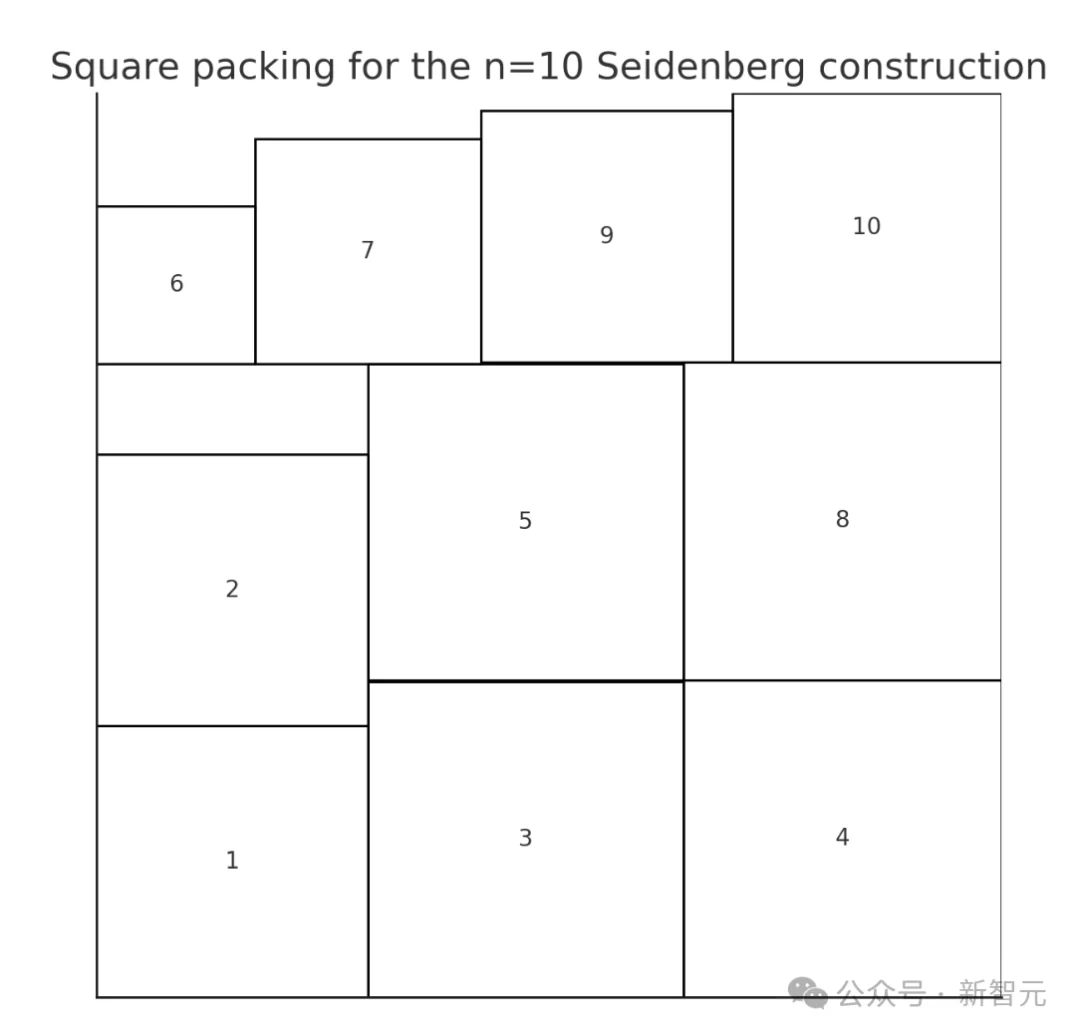
理由：对任意序列，可构造一系列正方形，它们互不重叠地填满边长为S(x1,…,xn)的大正方形。

下图展示了从AlphaEvolve给出的一个序列构造出的正方形填充。

最后一击

文献中的完整解

Lawrence再用AI深度搜索，找到了2024年Baek、Koizumi、Ueoro的论文，其中证明：f(k2+2c+1)≤k+c/k。

结合Praton的嵌入论证，这恰好给出：c(k2+2a+1)≤k/(k2+a)。

上下界再次吻合，猜想完全得证！

AI+人类

48小时极限突围

这个故事最让陶哲轩触动的一点是，能汇聚一群不同背景的人、文献和工具来攻克这个问题，是何等重要。

陶哲轩感慨道：

传统模式下，一两位数学家凭借简单工具，或许最终也能拼出全貌，但那可能需要数周甚至数月。而在这个协作网络中，所有关键环节在48小时内汇聚。

要陈述并证明c(n)的精确公式，需要基于多个观察结果，大概包括以下几点：

• 该序列可以被数值计算为有理数序列。
• 经过适当的归一化和排列后，序列中会出现肉眼可见的规律，让人能推测出序列的形式。
• 这个问题是Erdős-Szekeres定理的一个加权版本。
• 在Erdős-Szekeres定理的众多证明中，1959年Seidenberg的证明可以被解释为一种离散矩形填充论证。
• 这个问题可以被重新解释为连续正方形填充问题，实际上与Erdős问题106（关于此类填充）的（广义轴平行形式）密切相关。
• Erdős问题106的轴平行形式最近刚被Baek-Koizumi-Ueoro解决。
• Praton的论文表明，Erdős问题106蕴含了这个问题所需的广义版本。这个蕴含关系特指轴平行的情况。

正是靠着所有贡献者的通力合作以及他们使用的工具，所有这些关键线索才得以在48小时内汇集在一起。

如果换作传统的模式，只靠一两个数学家以及更简单的编程和文献搜索工具，虽然理论上最终也能把这些碎片拼凑起来，但这个过程会花长得多的时间（可能是数周甚至数月）。

另一个关键因素是Erdős问题网站上「平衡的AI政策」，它鼓励公开说明AI的使用情况，同时强烈反对隐瞒使用——

允许使用AI辅助编写评论，前提是：

（a）已对此进行公开说明；

（b）内容（包括数学推导、代码、数值数据及相关来源的存在性）已由用户自己在没有AI协助的情况下仔细核查与验证；

（c）评论篇幅在合理范围内，不过于冗长。

一道悬置50年的问题，在2025年的冬天，因为一次跨人机、跨时空的奇妙协作，终于画上了圆满的句号。

而这，可能只是一个新时代的开始。

参考资料：ZHB

https://terrytao.wordpress.com/2025/12/08/the-story-of-erdos-problem-126/

文章来自于微信公众号 “新智元”，作者 “新智元”