在人工智能快速发展的今天,大型语言模型(LLM)在各类任务中展现出惊人的能力。然而,当面对需要复杂推理的任务时,即使是最先进的开源模型也往往难以保持稳定的表现。现有的模型集成方法,无论是在词元层面还是输出层面的集成,都未能有效解决这一挑战。
微软研究院与韩国科学技术院(KAIST)的研究团队提出了一种创新的解决方案:基于过程奖励引导的蒙特卡洛树搜索的语言模型集成框架(LE-MCTS)。这一方法不仅在理论上开创性地将复杂推理问题形式化为马尔可夫决策过程(MDP),更在实践中展现出显著的性能提升。在过去一年里,我曾经给大家介绍过多篇关于MCTS和MDP的高级提示方法,您有兴趣可以翻翻之前的文章或下面赞赏分类的文章。
选择MCTS作为集成框架的理论依据主要有三点:
1.状态空间探索能力:MCTS通过树搜索可以有效探索大规模状态空间,这与复杂推理问题中需要考虑多个可能推理路径的特点高度契合。
2.动态决策机制:MCTS的选择-扩展-模拟-回传机制天然适合推理过程中的动态决策需求,可以根据当前状态灵活选择最优的语言模型和推理步骤。
3.理论保证:MCTS具有理论上的收敛性保证,随着搜索次数的增加,能够逐步逼近最优解,这为复杂推理任务提供了可靠的质量保证。
传统的语言模型集成方法主要分为两类:词元级别的集成和输出级别的集成。词元级别的集成试图合并多个模型的输出概率分布,但这种方法面临着词表不一致、模型架构差异等技术障碍,往往需要额外训练投影矩阵来克服这些问题。而输出级别的集成虽然可以应用于任何语言模型,但当所有候选输出都存在缺陷时,这种方法也无法产生正确的答案。研究团队通过大量实验证实,这些传统方法在解决复杂推理问题时的表现甚至不如单个语言模型,这凸显出在复杂推理任务中亟需一种新的集成范式。
LE-MCTS 的核心创新在于将推理过程分解为一系列步骤,并在每个步骤上动态选择最优的语言模型。这种方法将复杂推理问题形式化为马尔可夫决策过程,其中状态表示中间推理路径,动作则是使用预定义模型池中的某个模型生成下一个推理步骤。通过过程奖励模型的指导,LE-MCTS 能够在不同语言模型生成的推理步骤中进行树搜索,从而找到最优的推理路径。
让我们通过一个具体示例来理解 LE-MCTS 的工作原理:

1.问题展示区(顶部):
2.树形结构(中心区域):
3.推理步骤(右侧):
这个示例清晰地展示了多个语言模型如何协同工作,每个模型在最适合自己的推理步骤上发挥作用。
LE-MCTS 的实现包含以下关键组件:
1.状态表示:每个状态包含问题描述和当前的推理步骤序列。
2.动作空间:包含两个维度:选择哪个语言模型,以及该模型生成的具体推理步骤。
3.奖励机制:使用预训练的过程奖励模型(PRM)评估每个推理步骤的质量。
4.树搜索策略:采用改进的 PUCT(Predictor + UCT)算法来平衡探索与利用。
LE-MCTS 框架中单次迭代的完整流程,通过四个关键阶段清晰地展示了算法的工作机制。
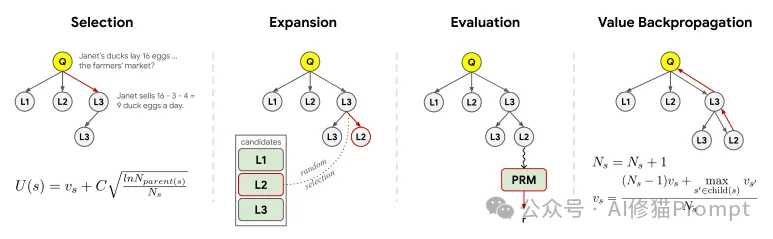
1.选择阶段(Selection,最左侧)
2.扩展阶段(Expansion,左中位置)
3.评估阶段(Evaluation,右中位置)
4.价值回传阶段(Value Backpropagation,最右侧)
LE-MCTS 的具体实现可以通过以下伪代码来理解:

1.输入与初始化 (第1-3行)
2.选择阶段 (第4-12行)
3.扩展阶段 (第13-18行)
4.评估与价值回传 (第19-24行)
5.输出处理 (第25-26行)
为了进一步提升系统性能,研究团队对价值回传策略进行了创新性优化。传统的MCTS使用平均值回传策略,这在语言模型集成场景下存在局限性:
1.传统策略的局限:
2.优化回传策略的创新:
3.理论优势:
实验结果验证了优化回传策略的效果:
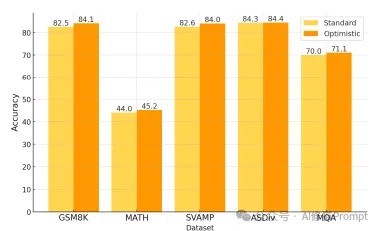
实验分析:
1.数据集表现:
2.效果分析:
研究团队在五个广泛使用的数学推理数据集上进行了实验:GSM8K、MATH、SVAMP、ASDiv 和 MQA。这些数据集涵盖了不同难度和类型的数学问题,从小学级别的应用题到高中级别的代数问题。实验中使用了多个主流的开源语言模型,并与现有的各类集成方法进行了全面对比。
研究团队为不同数据集设计了精心的提示词来生成合成测试数据。这些提示词的设计体现了作者在保持数据质量和多样性方面的深入考虑。
1.GSM8K数据集提示词设计 作者为GSM8K数据集设计的提示词聚焦于日常生活中的应用数学问题。提示词要求生成16个与示例难度、技能要求和风格相匹配的数学问题。示例问题涉及:
2.MATH数据集提示词设计 针对MATH数据集的提示词展现了更高的技术复杂度,包含:
3.SVAMP数据集提示词设计 SVAMP数据集的提示词设计体现了对基础数学问题变体的关注:
4.ASDiv数据集提示词设计 ASDiv数据集的提示词设计突出了基础教育场景下的数学问题特点:
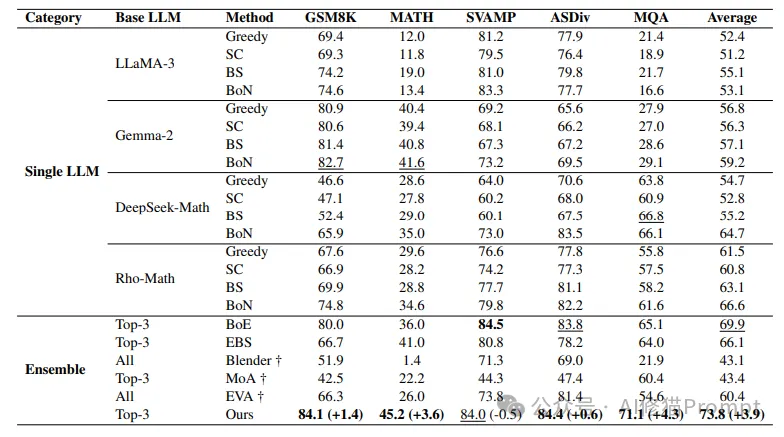
1.行类别划分:
2.列类别划分:
1.单模型性能:
2.集成方法性能:
1.方法优势:
2.一致性表现:
3.改进效果:
1.分步推理的重要性:
2.模型选择策略:
3.提示词设计:
1.依赖过程奖励模型:系统的性能很大程度上依赖于过程奖励模型的准确性。当 PRM 无法准确计算奖励时,LE-MCTS 的效果也会受到影响。虽然在已建立的数学数据集上表现良好,但面对全新的数学问题时,现有的 PRM 可能无法保证同样的性能。
2.基础模型选择:实验结果表明,使用较弱的基础模型会影响 LE-MCTS 的整体性能。虽然可以通过少量合成数据来识别较弱的基础模型,但这种方法在其他任务和数据集上的泛化性还需要进一步验证。
1.通用性提升:如何将这种方法扩展到其他类型的复杂推理任务,特别是那些缺乏明确评估标准的领域。
2.效率优化:在保持性能的同时,如何降低计算开销,使系统能够在更多实际应用场景中发挥作用。
3.鲁棒性增强:如何提高系统在面对噪声数据和异常情况时的稳定性。
LE-MCTS 的提出为解决复杂推理任务提供了一个全新的思路。通过将推理过程分解为一系列步骤,并在每个步骤上动态选择最优的语言模型,这种方法显著提升了系统在复杂推理任务上的表现。对于 Prompt 工程师而言,这项研究不仅提供了直接可用的技术方案,更重要的是提供了一种新的思维方式:将复杂问题分解为可控的步骤,并在每个步骤上进行优化。虽然目前还存在一些局限性,但随着相关技术的不断发展,这种方法的应用前景将更加广阔。
文章来自于“AI修猫Prompt”,作者“AI修猫Prompt”。

【免费】cursor-auto-free是一个能够让你无限免费使用cursor的项目。该项目通过cloudflare进行托管实现,请参考教程进行配置。
视频教程:https://www.bilibili.com/video/BV1WTKge6E7u/
项目地址:https://github.com/chengazhen/cursor-auto-free?tab=readme-ov-file
【开源免费】LangGPT 是一个通过结构化和模板化的方法,编写高质量的AI提示词的开源项目。它可以让任何非专业的用户轻松创建高水平的提示词,进而高质量的帮助用户通过AI解决问题。
项目地址:https://github.com/langgptai/LangGPT/blob/main/README_zh.md
在线使用:https://kimi.moonshot.cn/kimiplus/conpg00t7lagbbsfqkq0