陶哲轩亲测点赞，o3-mini秒证图论难题！专家级证明完整呈现

o3-mini成功挑战图论中专家级证明，还得到了陶哲轩盛赞。经过实测后，他总结称LLM并非是数学研究万能解法，其价值取决于问题得性质和调教AI的方式。

o3-mini竟然已经进化到，能秒解图论难题的程度了？！

今天，陶哲轩在社交平台上，再次分享了自己用AI辅助数学证明的经典用例和感想。

他以Ruzsa-Szemeredi的「三角移除引理」（Triangle Removal Lemma）为例，目标是证明一个对专家来说图论中的标准结论：

一个由n个顶点、n个诱导匹配构成的图，其边数仅为o(n^2)

若要证明这个定理，有三种选择：用笔和纸自己手动推导；通过网络搜索找答案；或借助大模型。

在此，陶哲轩明智地采用了第三种方式，让o3-mini去证明。

结果令人眼前一亮，几秒钟内，AI给出了一个正确的答案，一个精准且清晰的推导过程，完美阐释出「三角移除引理」如何限制了边数。

那么，o3-mini是如何做到的呢？

ChatGPT秒解图论难题

陶哲轩向o3-mini发起提问：

Ruzsa-Szemerédi三角形移除引理表明，如果一个有n个顶点的图（当n很大时）仅包含o(n^3)个三角形，则可以通过移除o(n^2)条边使其变为无三角形图。显然，该引理隐含了这样一个结论：如果一个n顶点的图是n个诱导匹配（induced matching）的并集，则其总边数仅为o(n^2)。你知道如何从前者推出后者吗？

经过30秒思考过程，o3-mini给出了证明的关键思路——

通过在辅助图中将诱导匹配的边「编码」为三角形，然后再应用三角形移除引理。

而大致思路是，首先诱导匹配的并集，构造一个辅助的三部图，然后关联边数和三角形数，最后再应用三角形移除引理。

这个答案，让陶哲轩非常满意。

「AI能够满足我的即时需求，这表明LLM在快速提供某一领域内标准论证的细节方面，是一个优秀的用例，用户可以随后验证其正确性」。

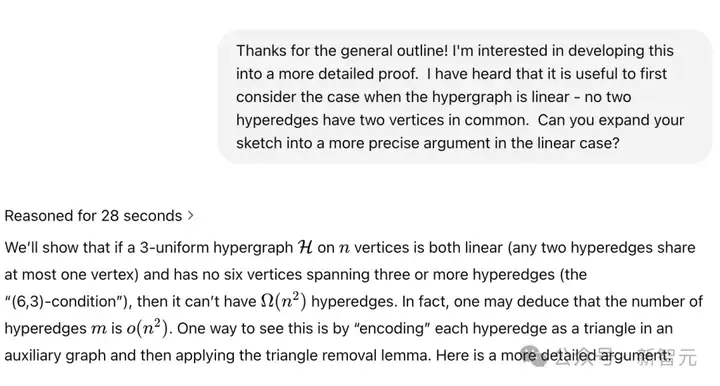
紧接着，他进一步询问模型，关于三角移除引理的另一标准推论—— Ruzsa-Szemeredi (6,3)定理。

该定理涉及三均匀超图，在特定禁止配置下的规模限制。

这一次，模型的表现却不尽如人意。

最初的回答虽抓住了用超图编码一个图的总体思路，但缺乏所有的关键细节。

当陶哲轩进一步追问时，它没有提到两个最重要的思路：

• 利用 (6,3) 条件来限制编码图中不需要的三角形
• 最初简化为线性超图的步骤

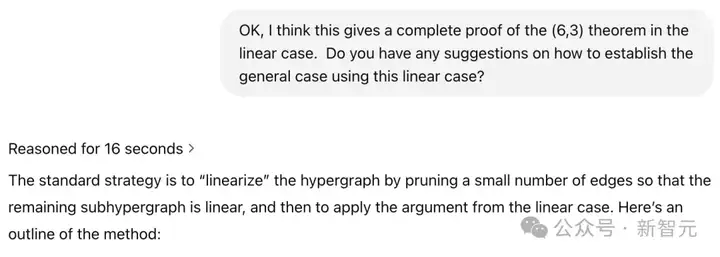
经过多次提示和明确的引导下，o3-mini才逐渐补全思路，最终给出了一个基本正确的推导证明。

陶哲轩表示，自己之所以能够给出提示，也是因为事先通过上网搜索查阅了证明。

如下是，为了得到详细证明，更加明确的提示。

个人感想

通过这次亲测，陶哲轩对LLM在数学研究中的能力，给出了自己的观察。

他表示，对于那些教科书级别的标准问题，模型的表现近乎完美，几乎无需干预。

这些答案基本可以从维基百科、StackOverflow等现有资源中找到。

然而，当问题转向研究级别，或较少被讨论的领域时，模型的成功率显著下降。

他将LLM的能力概括为两种状态：

一种是在宽泛指导下仍能提供有价值的帮助；另一种则需要用户详细引导，甚至更高计算资源才能逐步完善答案。

最强大的模型或许更倾向于前者，但整体而言，随着问题复杂度和岭门程度增加，LLM的表现逐渐减弱。

AI辅助数学研究，提前到来

在评论区，网友们讨论一片，有人疑惑地表示，「尽管网络搜索质量有所下降，但它仍比AI工具在最好和最坏的情况下，都能提供准确的结果。那么，这种工具的意义何在」？

他表示，自己唯一能想到使用这种工具的理由，便是用它来获取新事物的灵感。

陶哲轩解释道，「目前，我认为LLM查询在最佳情况下优于网页搜索，因为其响应速度更快且更符合需求；相比于构造搜索查询、浏览多个搜索结果以判断哪些最有价值，然后将最佳结果的答案转换为自己应用所需的符号和上下文，创建提示并阅读LLM的响应，所需的脑力负担更小。然而，在最坏情况下，这类查询可能比传统搜索更耗费心力」。

因此，目前这两种方法在实用性上大致相当，至少对于查找相对知名的技术性论证而言。

当前的最佳解决方案似乎是采用混合方法，即首先向LLM提问，但如果其答案不能立即令人满意，则切换到其他方法（如网页搜索），或者利用网页搜索提供的线索进一步向LLM提问。

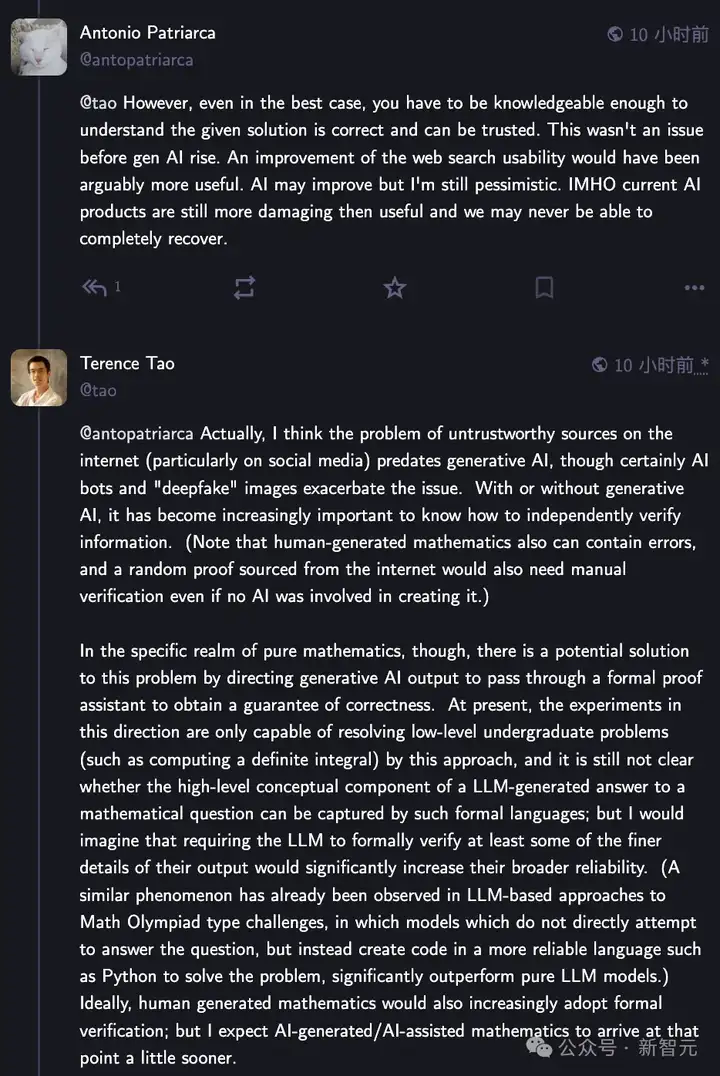
这位网友再次问道，「即使在最佳情况下，用户仍需具备足够的知识来判断给出的解决方案是否正确且可信。在GenAI出现之前，这并不是一个问题。提升网页搜索的可用性或许会更加有用。尽AI可能会改进，但我仍然持悲观态度。在我看来，当前的AI产品总体上弊大于利，我们可能永远无法完全恢复。

陶哲轩表示，事实上，我认为互联网（尤其是社交媒体）上不可靠信息的泛滥早于生成式AI的兴起，尽管AI机器人和「深度伪造」图像确实加剧了这一问题。

无论是否有生成式AI，独立验证信息的能力正变得愈发重要。（需要注意的是，人类创作的数学也可能包含错误，即便没有AI介入，来自互联网的随机证明仍然需要人工验证。）

然而，在纯数学领域，这个问题或许有一个潜在的解决方案，即要求生成式AI通过形式化证明助手来验证其输出，以确保正确性。

目前，这方面的实验仅能解决低阶本科水平的问题（例如计算定积分），尚不清楚LLM生成的数学答案中涉及的高阶概念是否可以通过这种形式语言捕捉。

陶哲轩认为，要求LLM至少形式化验证其部分细节，能够显著提高其整体可靠性。（类似的现象已在LLM处理数学奥林匹克竞赛类型问题时被观察到——相比于直接生成答案，模型若采用更可靠的语言（如 Python）编写代码来求解问题，通常能显著优于纯LLM方法。）

理想情况下，人类创作的数学也应当越来越多地采用形式验证；但我预计AI生成或AI辅助的数学研究会提前实现这一点。

当然，评论区也有质疑大模型推理能力的网友，认为LLM并非是推理模型，而是随机文本生成器。

参考资料：

https://mathstodon.xyz/@tao/114139125505827565

文章来自于“新智元”，作者“桃子”。