原来Scaling Law还能被优化？Meta这招省token又提效

2017 年，一篇《Attention Is All You Need》论文成为 AI 发展的一个重要分水岭，其中提出的 Transformer 依然是现今主流语言模型的基础范式。尤其是在基于 Transformer 的语言模型的 Scaling Law 得到实验验证后，AI 领域的发展更是进入了快车道。

现如今，这篇论文的引用量正向 19 万冲刺，而 Transformer 和注意力机制本身也已经历了很多改进和创新，比如我们前段时间报道过的「Multi-Token Attention」和「Multi-matrix Factorization Attention」等。

随着 AI 的不断发展，现如今的一个重要挑战是如何获得足够多高质量的 token。又或者，该如何更高效地利用这些 token？为此，还必须对 Transformer 进行进一步的升级改造。

近日，Meta 的一篇论文公布了他们在这方面取得的一个新进展，提出了一种旋转不变型三线性注意力机制，并证明其表示能力与 2-simplicial Transformer 相当。更重要的是，它的表现甚至足以改变 Scaling Law 中的系数。Meta 也用 Triton 实现了这种注意力机制。

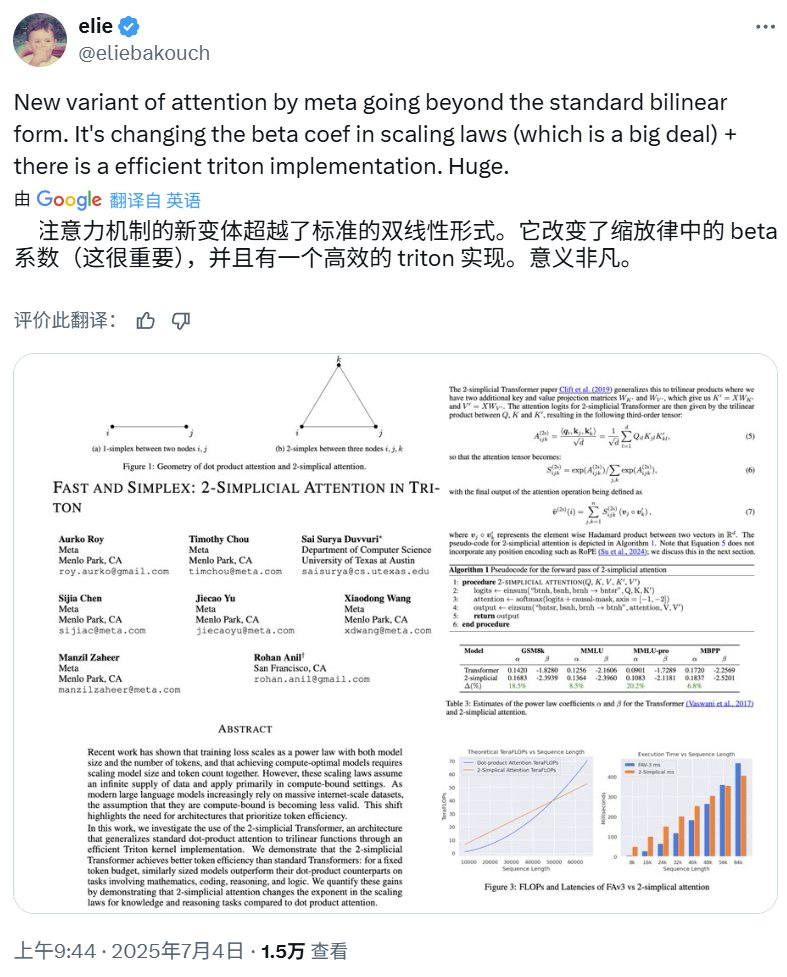
该研究基于 RoPE 向三线性函数的泛化；而 2-simplicial Transformer 则源自 2019 年 Clift et al. 的研究《Logic and the 2-Simplicial Transformer》，其中将 Transformer 的点积注意力机制泛化到了三线性形式。

• 论文标题：Fast and Simplex: 2-Simplicial Attention in Triton

• 论文地址：https://arxiv.org/pdf/2507.02754.pdf

他们进一步证明，在有限的 token 预算下，2-simplicial Transformer 的扩展性优于 Transformer。

此外，他们的实验还表明，2-simplicial Transformer 相对于 Transformer 具有更有利的参数数量 scaling 指数。这表明，与 Chinchilla scaling 不同，有可能以比 2-simplicial Transformer 的参数增长更慢的速度增加 token 数量。

研究结果表明，在 token 约束下运行时，与点积注意力机制 Transformer 相比，2-simplicial Transformer 可以更有效地逼近自然语言的不可约熵。

神经 Scaling Law 概述

要理解这项研究的意义，首先需要了解一下 Scaling Law。

对于给定的计算预算 C，其中 FLOPs (N, D) = C，可以将最佳参数数量表示为 N_opt ∝ C^a，将最佳数据集大小表示为 D_opt ∝ C^b。Hoffmann et al. (2022) 进行了多次实验，并根据损失拟合了参数函数，以估计指数 a 和 b。

结果，通过多种不同方法发现：a 约为 0.49，b 约为 0.5。

如此，便引出了 Hoffmann et al. (2022) 的一个核心论点：必须根据模型大小按比例扩展 token 数量。

但是，正如前面讨论的那样，足够高质量且足够数量的 token 是预训练扩展的新瓶颈，因此需要探索替代的训练算法和架构。另一方面，最近的研究表明，之前文献中提出的大多数建模和优化技术仅仅改变了误差（偏移了 E），并没有从根本上改变幂律中的指数。谷歌 DeepMind 的研究者 Katie Everett 对此进行过精彩的讨论：

https://x.com/_katieeverett/status/1925665335727808651

添加图片注释，不超过 140 字（可选）

2-simplicial Transformer

2-simplicial Transformer 由 Clift et al. (2019) 提出，他们将点积注意力机制从双线性扩展为三线性形式，也就是从 1-simplex 扩展成了 2-simplex。

基于行列式的三线性形式

Su et al., 2024 提出 RoPE 时，是想将其作为一种用于 Transformer 语言模型的序列位置信息捕获方法。RoPE 对查询 q_i 和键 k_j 应用位置相关的旋转，使得点积 <q_i, K_j> 是相对距离 i-j 的函数。特别需要注意的是，点积对于正交变换 R 具有不变性：

这对于 RoPE 至关重要，因为对于同一位置 i 相同的查询 q_i 和键 k_i，我们期望其点积不会因基于位置的旋转而发生变化。请注意，(5) 式中定义的三线性形式并非是旋转不变，并且对 q_i 、k_i 和 k′_i 进行相同的旋转不再保留内积。因此，为了将 RoPE 泛化到 2-simplicial 注意力模型，探索其他具有旋转不变性的双线性和三线性形式至关重要。

而 Meta 的这个团队注意到，以下函数也具有旋转不变性：

模型设计

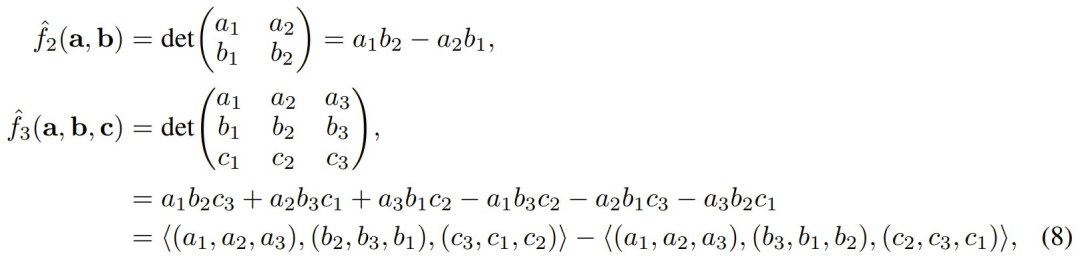
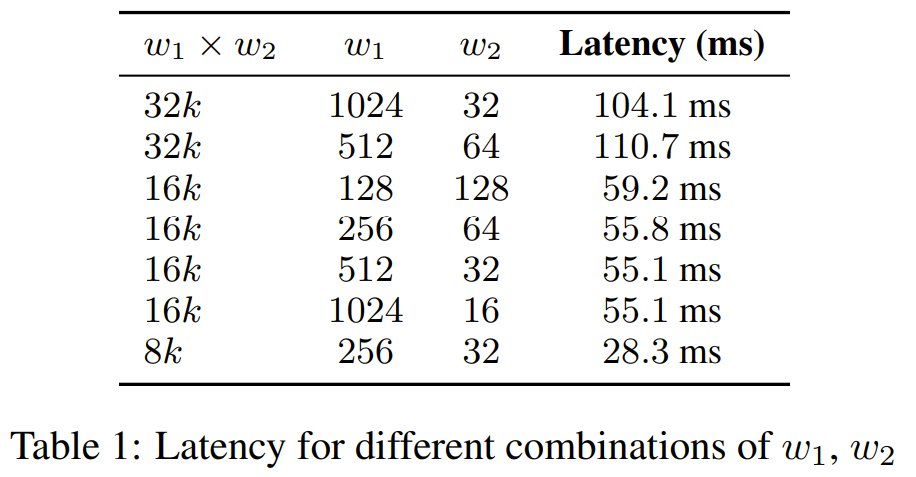
由于 2-simplicial 注意力在序列长度 n 上的扩展复杂度为 O (n^3)，因此将其应用于整个序列是不切实际的。该团队的做法是将其参数化为 O (n× w_1 × w_2)，其中 w_1 和 w_2 定义的是序列上滑动窗口的维度。每个查询向量 Q_i 会关注 w_1 个 K 键和 w_2 个 K′ 键的局部区域，从而减轻计算负担。该团队系统地评估了 w_1 和 w_2 的各种配置，以确定计算效率和模型性能之间的最佳平衡点（见表 1）。

对于因果点积注意力机制，长度为 n 的序列的复杂度由下式给出：

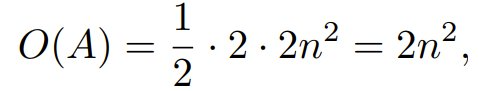
其中 n 是序列长度。这涉及两次矩阵乘法：一次用于 Q@K，一次用于 P@V，每次乘法每个元素都需要两次浮点运算。因果掩码使其能够跳过 1/2 的计算。

相比之下，以 w_1 和 w_2 为参数的 2-simplicial 注意力机制的复杂度表示为：

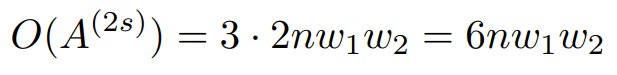
其复杂度的增长来源是三线性 einsum 运算，与标准点积注意力机制相比，它需要进行一次额外的乘法运算。

该团队选择窗口大小为 (512, 32)，以平衡延迟和质量。在此配置下，2-simplicial 注意力机制的计算复杂度与 48k 上下文长度的点积注意力机制相当。

图 2 给出了一个实现。因此，像在 Flash 注意力机制中那样平铺式查询 Q 会导致计算吞吐量较低。受 Native Sparse Attention 的启发，Meta 该团队采用的模型架构利用了较高 (64) 的分组查询注意力 (GQA) 比率。这种方法能够沿着查询头高效地平铺，确保密集计算，并消除昂贵的逐元素掩码。

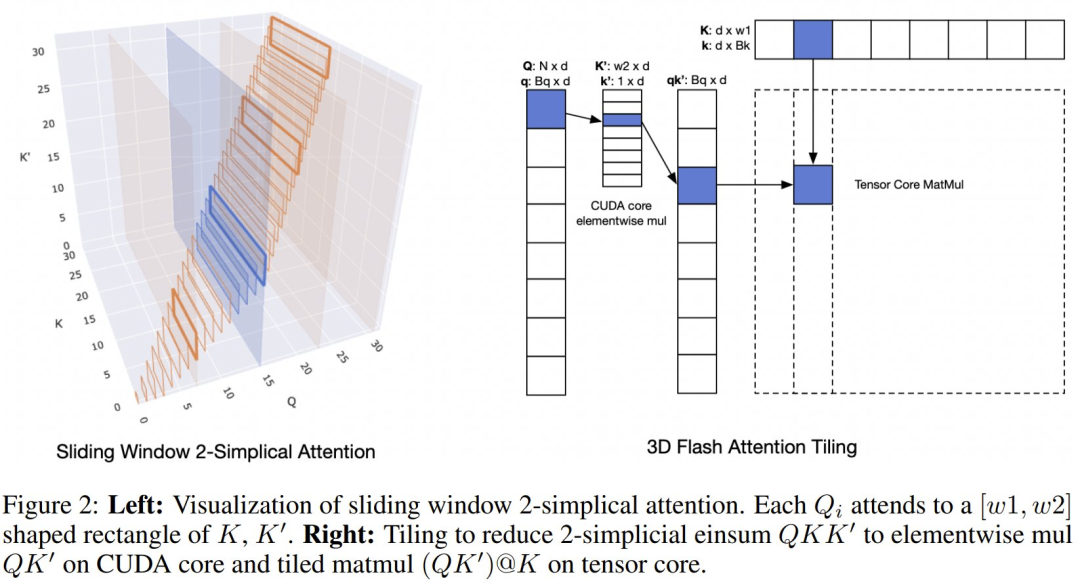
该团队还引入了一系列针对 2-simplicial 注意力的核优化，这些优化基于使用在线 softmax 的 Flash Attention。详见原论文。下面来重点看看实验表现。

实验与结果

这个团队训练了一系列 MoE 模型，其参数范围从 1B 活动参数和 57B 总参数到 3.5B 活动参数和 176B 总参数。具体配置见原论文。

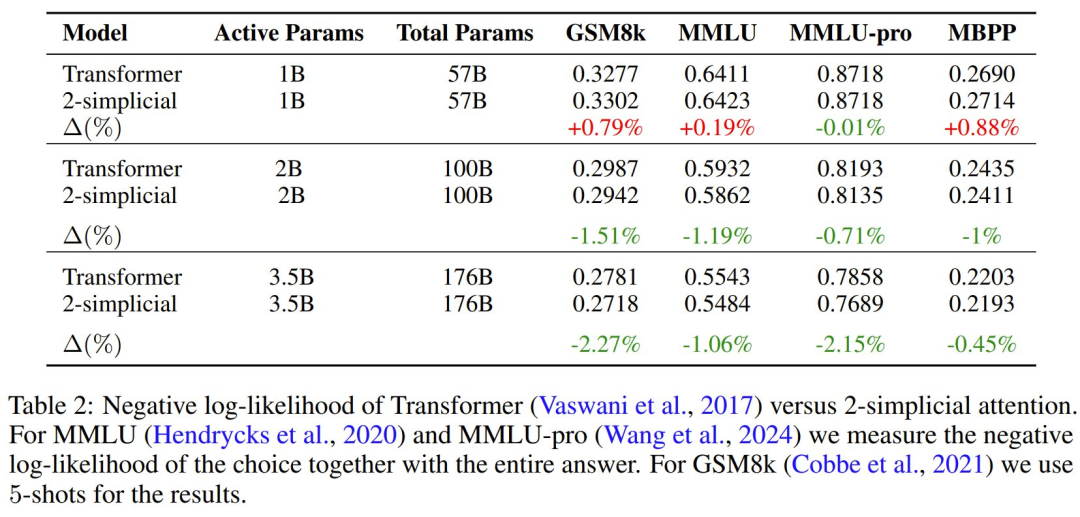
该团队发现，从 1B （活动）参数模型到 3.5B （活动）参数模型，负对数似然的扩展（∆）出现了下降。

此外，在小于 2B （活动）参数的模型中，使用 2-simplicial 注意力机制没有任何好处。

基于此，该团队估算了 2-simplicial 注意力机制与点积注意力机制的幂律系数有何不同。基于前述方法，其损失可以表示为：

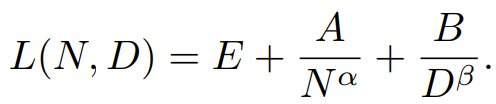
由于训练这两个模型使用的 token 数量相同，因此可以忽略第三项，将损失简化为：

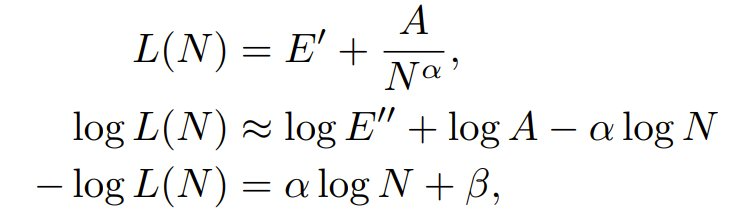
其中 β = - log E′′ - logA ，由于 E′ 较小，E′′ 是 E′ 的近似值。注意，这里使用了 log (a + b) = log (1 + a/b) + log (b) 来分离这两个项，并将 1 + a/b 项隐藏在 E′′ 中。

因此，可以根据表 2 中的损失估算两组模型的 α 和 β，其中 N 代表每个模型中的有效参数。

该团队在表 3 中估计了 Transformer 和 2-simplicial Transformer 的斜率 α 和截距 β。

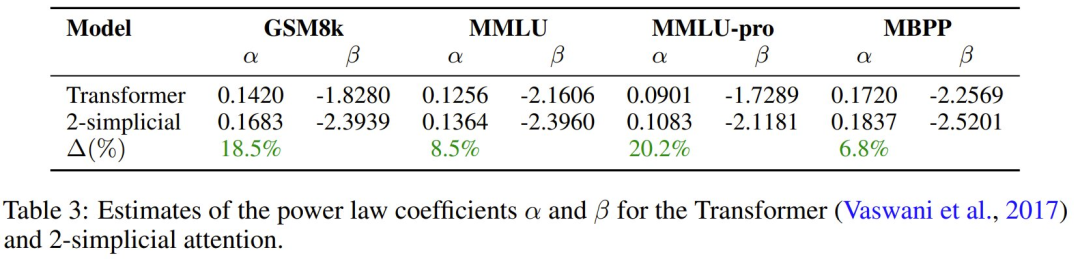
可以看到，与点积注意力 Transformer 相比，2-simplicial 注意力具有更陡的斜率 α，即其 Scaling Law 的指数更高。

文章来自于微信公众号“机器之心”。