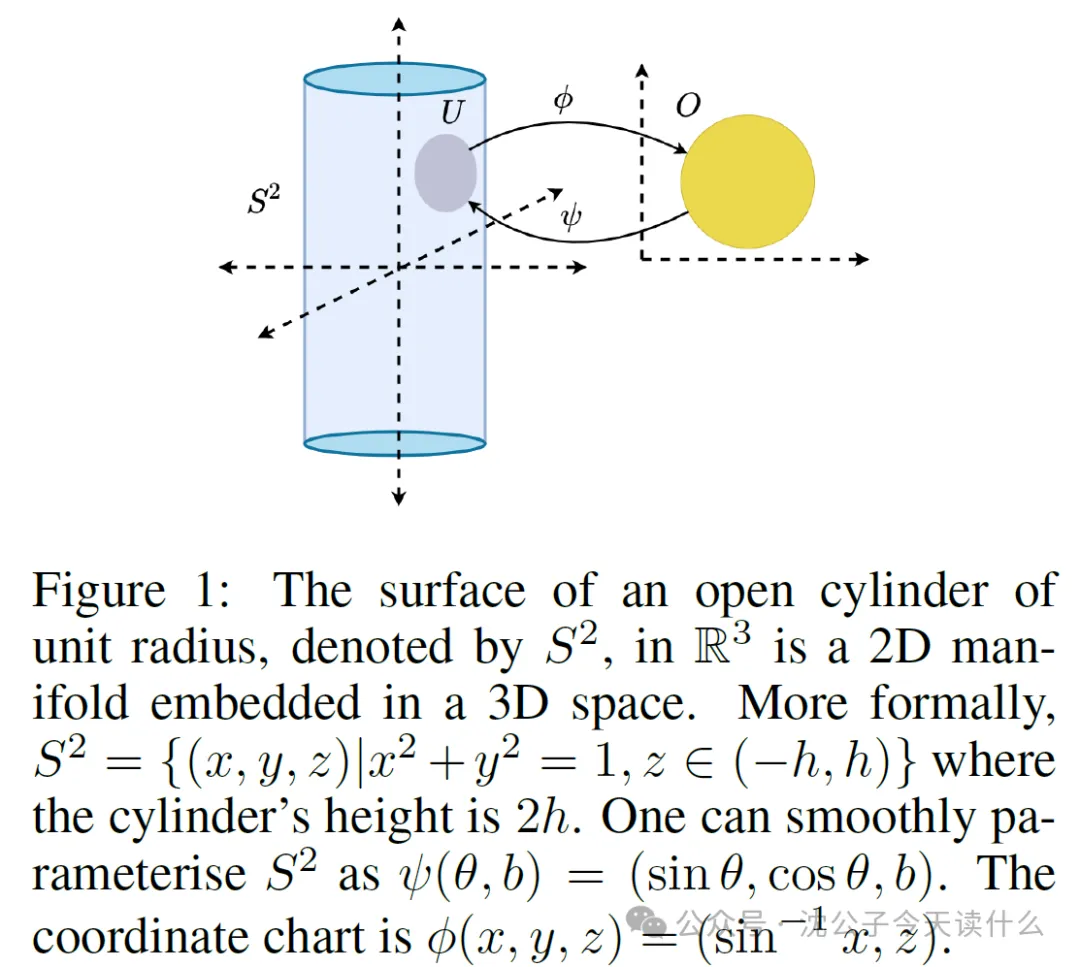
一句话概括,原来强化学习的“捷径”是天生的,智能体能去的地方(流形)被动作维度(低维流形)限制得死死的,根本没机会去那些没用的高维空间瞎逛。(原论文题目见文末,点击阅读原文可直接跳转至原文链接, Published on ICLR on 28 Jul 2025, by Brown University)
亲爱的读者们,沈公子的公众号agent和base model升级到v3.0,今后公众号文章行文会更流畅,处理公式和符号也完全达到人类专家水准,会大幅减少出现错乱和显示异常的情况,提升阅读体验。enjoying :)
第一阶段:识别核心概念
论文的motivation分析
想象一下,我们教一个机器人(强化学习智能体)在复杂的虚拟世界里学走路。这个世界的“状态”可能极其复杂,比如机器人身上每个关节的角度、速度、加速度,以及它在三维空间中的位置和姿态等等,这些变量加起来可能有成百上千个维度,构成了一个庞大无比的“状态空间”。
然而,尽管状态空间如此巨大,我们发现机器人似乎总能学会走路、跑步、跳跃等任务。这就引出了一个核心问题:为什么强化学习能在这些看似“维度诅咒”缠身的复杂问题上取得成功? 难道智能体真的需要探索并理解这个成百上千维度的空间的每一个角落吗?
作者认为,答案是否定的。他们提出了一个直觉性的猜想,即智能体在学习过程中,实际能够到达和探索的状态集合,可能只是整个庞大状态空间中一个非常小的、结构化的子集。这个子集就像是辽阔沙漠中的一条蜿蜒小径。智能体并不需要在整个沙漠中漫无目的地游荡,只需要沿着这条小径探索,就能找到通往目的地的最佳路径。这篇论文的动机,就是为这个直觉性的猜想提供坚实的理论基础,并用实验加以验证。
论文主要贡献点分析
- 理论证明了可达状态流形的存在:论文首次从理论上证明,在连续状态和动作空间中,由一种常见的神经网络策略(宽幅两层网络)和训练算法(演员-评论家)驱动的强化学习智能体,其能够达到的状态集合,实际上位于一个低维度的“流形”(Manifold)上。
- 给出了维度的上界:更关键的是,论文证明了这个低维流形的维度主要由动作空间的维度()决定,其上界大约是 。这意义非凡,因为它表明了问题的内在复杂度与智能体的“控制能力”(有多少个动作维度)直接相关,而不是与环境的“描述复杂度”(状态空间的维度)相关。
- 提出了新的分析工具和模型:论文将微分几何和控制理论中的工具(如矢量场、李级数)引入到强化学习的理论分析中,为理解神经网络策略的行为提供了一套新的数学语言。
- 验证并应用了该理论:论文不仅停留在理论,还通过实验验证了这一发现,并基于此改进了现有算法,通过引入一个能够学习稀疏低维表示的“稀疏化层”,在一些高维控制任务上取得了显著的性能提升。
- 几何与控制理论的视角:论文的核心是将智能体的策略看作一个矢量场,这个场决定了在状态空间中每一点的前进方向。智能体的运动轨迹则是沿着这个矢量场行进的结果。
- 线性化的宽神经网络模型:为了让理论分析成为可能,论文采用了在深度学习理论中很常见的“线性化宽神经网络”模型。在这个模型下,复杂的神经网络动力学可以被简化,便于数学推导。这类似于在研究复杂曲线时,我们先看它在某一点的“切线”(一阶近似)。
- 李级数展开:为了分析智能体在短时间内的运动轨迹,论文使用了李级数来近似这个轨迹。这是一种比泰勒展开更适合描述矢量场驱动的系统动态的数学工具。
- 连续时间随机梯度动力学:论文将离散的、随机的参数更新过程(SGD)抽象为连续时间的随机微分方程,从而能在数学上分析策略参数的演变及其对可达状态集的影响。
理解难点识别
- 流形:这是贯穿全文的核心概念。读者需要理解什么是流形,为什么说它是“低维的”,以及它如何“嵌入”在高维空间中。
- 矢量场与指数映射:这是论文用来描述策略和轨迹的数学语言。需要理解策略如何等价于一个矢量场,以及状态的演化如何通过指数映射来描述。
- 线性化神经网络:这是理论推导得以进行的前提假设。需要明白这是一种什么样的简化,以及它和真实神经网络的区别与联系。
- 流形的直观理解与数学定义:对于没有微分几何背景的读者来说,“流形”本身就是一个抽象且难以捉摸的概念。论文中涉及的“微分同胚”、“坐标图卡”、“切空间”等术语会进一步增加理解难度。
- 李级数的作用:将策略(矢量场)和轨迹(曲线)联系起来,并分析其二阶项,从而揭示维度约束的来源,是论文推导的精华所在,也是最难理解的部分。
- 解释重点——为什么智能体有限的“动作”会导致其探索的状态局限在一个低维流形上。这是连接所有技术点的枢纽。
概念依赖关系
- 起点:一切始于强化学习在连续高维空间中面临的挑战。
- 核心假设:作者引入流形假设,认为智能体实际探索的是一个低维流形。
- 建模工具:为了证明这一点,作者将智能体的神经网络策略建模为一个矢量场。
- 分析方法:使用李级数来分析由该矢量场产生的状态轨迹。
- 关键洞察:通过分析李级数的前几项,发现轨迹的局部“延展方向”受到动作空间维度的严格限制。
- 最终结论:这些受限的轨迹共同构成了可达状态的低维流形,其维度上界被动作维度所约束。
- 切入点:最佳的切入点就是流形这个概念本身。可以用一个生动的生活化比喻来解释什么是流形,然后自然地引出:在强化学习中,这个流形是如何被智能体的“动作”创造出来的。
第二阶段:深入解释核心概念
设计生活化比喻:雕刻师与木块
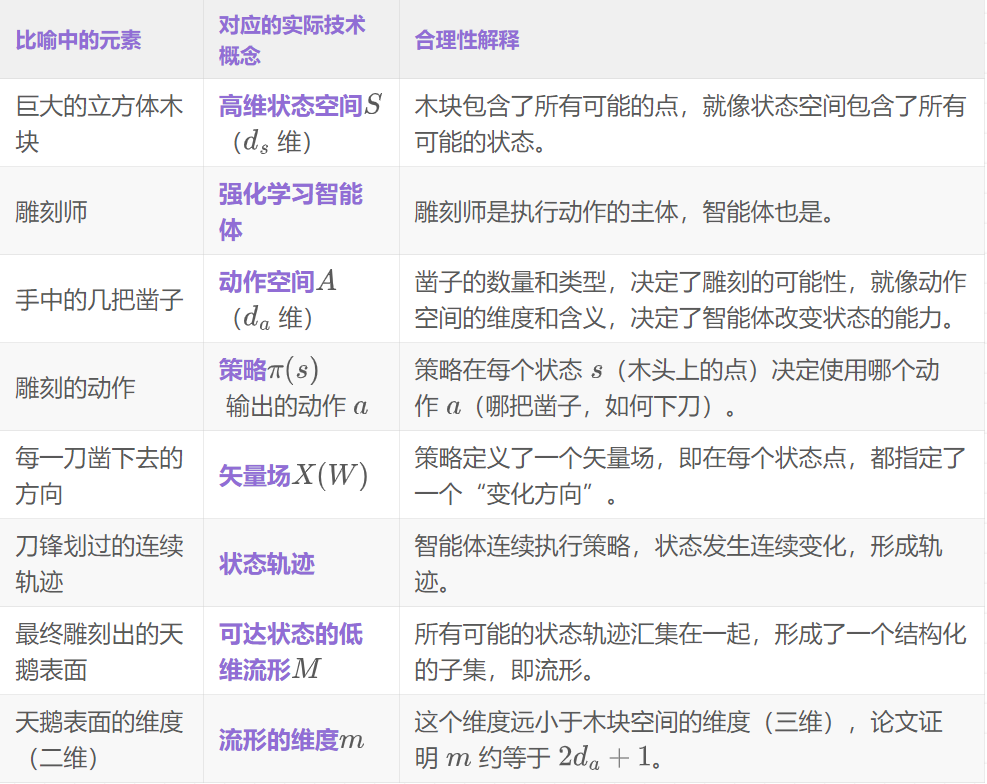
- 场景选择想象一位雕刻师,他得到了一块巨大的、未经雕琢的立方体木块。这块木块代表了环境中所有可能状态组成的高维状态空间。木块的每一个点都对应一个具体的状态。雕刻师的任务是在这块木块上雕刻出一只精美的天鹅。
- 核心机制雕刻师手头有几把工具:一把平口凿、一把圆口凿和一把斜口凿。这几把凿子,就代表了智能体的动作空间。比如,假设动作空间是3维的,那就对应这3把不同的凿子。
- 雕刻师不能凭空在木块内部任意一点进行雕刻,他必须从木块的某个表面(初始状态)开始。他的每一个动作,就是选择一把凿子(选择一个动作),朝着某个方向,以一定的力度和角度,从当前位置的木头表面凿下去。
- 这个比喻直观地展示了:一个拥有有限工具(低维动作空间)的创作者(智能体),在一个巨大的原材料(高维状态空间)上进行创作,其最终能触及和创造出的形态(可达状态集),本质上是一个由其工具能力所限制的低维结构(流形)。
- 关键机制——运动受限于工具:雕刻师能创造的形状,完全受限于他手里的这几把凿子。他可以用平口凿削出平面,用圆口凿挖出弧线。无论他技艺多么高超,他都无法直接在木块内部凭空创造一个球体,他必须从表面一点点地“触达”那个位置。
- 关键机制——路径的连续性:雕刻的过程是连续的。每一刀都会在前一刀的基础上留下新的表面。天鹅的轮廓,就是由无数刀连续的雕刻轨迹(状态轨迹)所共同形成的。
- 关键机制——低维的创作:最终,雕刻出的天鹅虽然存在于三维的木块空间中,但天鹅的“表面”本身是一个二维的曲面。任何在天鹅表面的微小移动,都可以在一个二维的局部平面上被描述。这个天鹅表面,就是一个二维流形,它被“嵌入”到了三维的木块中。
建立比喻与实际技术的对应关系
深入技术细节
- 从比喻到原理在强化学习中,环境的动态变化可以用一个函数 来描述,表示在状态 执行动作 持续时间 后到达的新状态。当时间 极小时,这种变化的方向可以用一个矢量来捕捉。
- 论文将智能体的策略 看作一个矢量场。想象状态空间中充满了无数微小的箭头,每个状态点 都有一个箭头 指示着“下一步该往哪走”,这个箭头的方 向和长度就由策略 决定。
- 相关数学公式论文的核心推导依赖于李级数,它用来描述从一个点 出发,沿着矢量场 “流动”一小段时间 后会到达哪里。重点看它的二阶展开式:
- 原始数学形式一个由策略(参数为 )定义的矢量场 可以写作(简化形式):其中 是环境的自然动态, 是动作 产生的控制动态。
- 智能体从 开始,在 时间后的状态 可以用指数映射 来表示,其李级数展开近似为:其中 是 关于自身的李导数,代表了矢量场的二阶变化。
- 符号替换版本新状态 ≈当前状态+ 短暂时间 * (智能体在当前状态下由策略决定的“瞬时速度”矢量)+ 0.5 * 短暂时间的平方 * (这个“瞬时速度”矢量自身的变化率,即“加速度”项)+ ...
- 这个公式告诉我们,智能体短时间内能到达的位置,主要由几个部分决定:
1.零阶项:,即起点。
2.一阶项(速度项):。这个方向由策略 直接给出,其自由度受限于动作空间维度 。
3.二阶项(加速度项):。这是理解维度约束的关键!论文证明,这个“加速度”项的自由度也主要由 个基向量和学习动态决定。
1.建立模型:将策略 参数化为一个宽两层神经网络,并使用其线性化形式进行分析。
2.描述轨迹:使用李级数展开智能体的状态轨迹,保留到二阶项。
3.分析基向量:分析展开式中的一阶项和二阶项,发现它们都可以被一组数量有限的基向量线性表示。
4.计数维度:统计这些基向量的数量,发现总数约为 。
5.得出结论:任何局部可达状态都位于一个维度为 的空间内,这些局部空间拼接起来,就形成了一个低维流形。
技术细节与比喻的映射

- 比喻的局限性:这个比喻很好地解释了“约束”,但未能完全体现学习过程的“优化”和随机性。但就“可达状态集受动作约束”这一点而言,该比喻是高度贴切的。
总结
- 核心联系:就像雕刻师无法摆脱工具的限制一样,强化学习智能体也无法逃脱其动作空间的束缚。
- 对应关系:智能体的策略定义了在状态空间中的“雕刻方向”(矢量场),而李级数展开则告诉我们,这些方向的组合是有限的,其自由度(维度)被动作空间牢牢锁住。
- 关键数学原理:最终,智能体所有可能的状态轨迹汇集在一起,形成的不是一片混沌,而是一个精致的、低维的流形——就像木块上最终浮现出的那只二维表面的天鹅。
第三阶段:详细说明流程步骤
理论证明流程:从模型到结论
- 一个连续时间的马尔可夫决策过程:定义了环境的基本规则。
- 一个特定的策略网络结构:一个宽的、两层前馈神经网络。
- 一个特定的学习框架:基于半梯度的演员-评论家算法。
1.策略的线性化与矢量场化:首先,对神经网络策略进行线性化处理(如公式(7)),并将其视为一个矢量场 (如公式(10))。
2.轨迹的李级数展开:使用李级数对智能体从状态 出发的状态轨迹进行展开,并分析到二阶项。
3.学习动态的连续时间建模:将离散的随机梯度更新过程(公式(8))建模为一个连续时间的随机微分方程(SDE)。
4.分析基向量与维度约束:深入分析李级数展开式中的各项,证明它们都可以被一组数量约为 的基向量所张成。
- 核心定理(Theorem 1):智能体可达的状态集,会弱收敛并集中在一个维度 的流形 周围。
实验验证与应用流程
- 目标:验证“线性化神经网络”是对真实神经网络的合理近似。
- 流程:在Cheetah环境中,比较标准两层神经网络与线性化版本在不同网络宽度下的奖励差异。
- 结论:如图2所示,随着网络宽度增加,奖励差值趋近于0,证明了近似的合理性。
- 目标:在实际任务中估计状态集的内在维度,并验证其是否满足理论上界。
- 流程:在四个MuJoCo环境中,使用DDPG训练智能体,记录其经历的状态,并使用成熟的内在维度估计算法进行分析。
- 结论:如图3所示,在所有环境中,估计的内在维度(蓝色曲线)远低于状态空间维度(绿色线),且始终保持在理论上界 (红色线)之下,提供了强有力的经验证据。
- 目标:证明“可达状态是低维”的洞见可以用于改进算法性能。
- 流程:在SAC算法中,将一个标准全连接层替换为能利用低维结构的稀疏化层(如公式(12)),并在高维环境中进行比较。
- 结论:如图5所示,修改后的“稀疏SAC”(红色曲线)性能显著优于原始SAC(蓝色曲线),证明了理论洞见的实用价值。
第四阶段:实验设计与验证分析
主实验设计解读:核心论点的验证
- 核心主张:智能体可达状态集位于一个低维流形上,其维度由动作空间维度 决定,上界为 。
- 主实验设计:实验二,“可达状态的维度估计”,直接测量问题的内在几何结构。
- 数据集:作者选择了四个经典的MuJoCo连续控制任务,均为 的典型例子,与理论场景完美契合。
- 评价指标:估计的内在维度,直接度量核心主张,论证直接有力。
- 基线方法:环境的状态空间维度 和理论上界,通过与这两个“标尺”比较,清晰展示了结论。
- 主实验结论: 如图3所示,实验结果定量地、直观地证实了论文的核心理论主张。
消融实验分析:内部组件的贡献
- 实验一验证了“线性化宽网络”这一理论假设的合理性。
- 实验三验证了“利用低维几何结构”这一理论洞见的实用价值。
- 实验三中稀疏SAC的性能提升,定量地证明了利用低维流形洞见的必要性和优越性。
深度/创新性实验剖析:洞察方法的内在特性
- 巧妙实验——玩具线性环境中的维度验证(实验5.3)
- 实验目的:在一个理论上完全可控的环境中,展示其理论与经典控制理论结果的差异与联系。
1.构建一个根据经典控制理论是完全可控的线性系统。
2.应用论文的理论框架,限制策略为有界的神经网络,固定动作维度 ,增加状态维度 。
3.估计在神经网络策略下,可达状态集的内在维度。
- 实验结论: 如图4所示,一个惊人的结果出现了:尽管系统本身“完全可控”,但只要策略被限制在有界的神经网络函数族内,其可达状态的内在维度就不再随状态空间维度增加,而是被牢牢地“钉”在了理论上界 之下!
- 深刻洞见:这个实验漂亮地揭示了,问题的“内在复杂度”,不仅取决于环境动力学,还强烈地取决于我们用来解决问题的“函数类别”。
本文题目:GEOMETRY OF NEURAL REINFORCEMENT LEARNING IN CONTINUOUS STATE AND ACTION SPACES
文章来自于微信公众号“沈公子今天读什么”,作者是“Tensorlong 看天下”。


