一、标量、向量、矩阵、张量的关系

这4个概念是维度不断上升的，我们用点线面体的概念来比喻解释会更加容易理解：

• 点——标量（scalar）
• 
  
• 线——向量（vector）
• 
  
• 面——矩阵（matrix）
• 
  
• 体——张量（tensor）

一维向量：直线

二维向量：平面

三维向量：空间

N维...

二、标量 | scalar

标量只有大小概念，没有方向的概念。通过一个具体的数值就能表达完整。

比如：重量、温度、长度、提及、时间、热量等都数据标量。

三、向量 | vector

向量指具有大小和方向的量，形态上看就是一列数；

• 通常赋予向量粗体小写的名称；手写体则在字母上加一个向右的箭头。
• 
  
• 向量中的元素是有序排列的，通过索引可以确定每个元素。
• 
  
• 以下两种方式，可以明确表示向量中的元素时（注意用方括号）。
• 
  
• 可以把向量看作空间中的有向线段，向量的每个组成元素，对应向量在不同的坐标轴上的投影长度。
• 
  

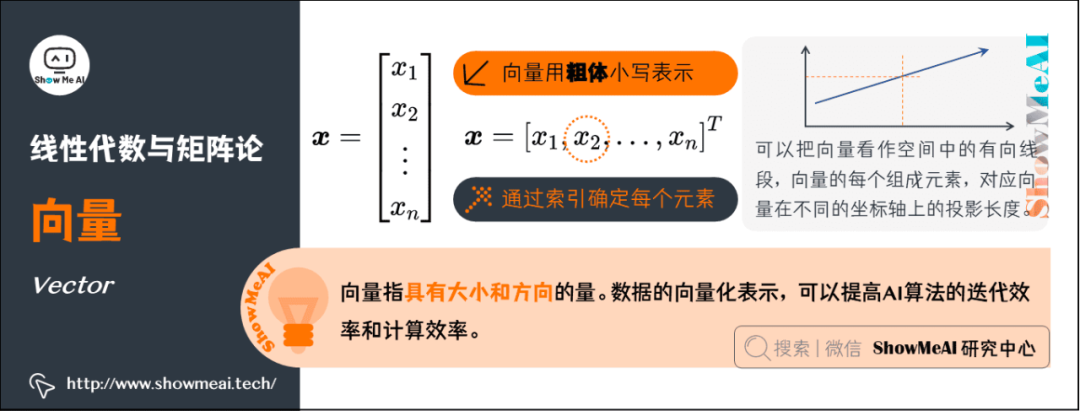
AI中的应用：在机器学习中，单条数据样本的表征都是以向量化的形式来完成的。向量化的方式可以帮助AI算法在迭代与计算过程中，以更高效的方式完成。

代数表示

一般印刷用黑体的小写英文字母（a、b、c等）来表示，手写用在a、b、c等字母上加一箭头（→）表示，如

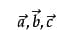
几何表示

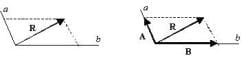
向量可以用有向线段来表示。有向线段的长度表示向量的大小，向量的大小，也就是向量的长度。

坐标表示

在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量i，j作为一组基底。a为平面直角坐标系内的任意向量，以坐标原点O为起点P为终点作向量a。由平面向量基本定理可知，有且只有一对实数（x,y），使得a=xi+yj，因此把实数对(x,y)叫做向量a的坐标，记作a=(x,y)。这就是向量a的坐标表示。其中(x,y)就是点 P 的坐标。向量a称为点P的位置向量。

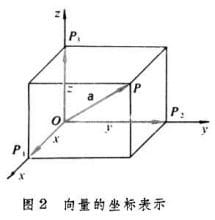
在空间直角坐标系中，分别取与x轴、y轴，z轴方向相同的3个单位向量i，j，k作为一组基底。若为该坐标系内的任意向量，以坐标原点O为起点作向量a。由空间基本定理知，有且只有一组实数(x,y,z)，使得a=ix+jy+kz，因此把实数对(x,y,z)叫做向量a的坐标，记作a=(x,y,z)。这就是向量a的坐标表示。其中(x,y,z)，就是点P的坐标。向量a称为点P的位置向量。

当然，对于多维的空间向量，可以通过类推得到。

向量的矩阵表示

四、矩阵 | Matrix

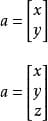
矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。矩阵是二维数组，其中的每一个元素被两个索引确定。矩阵在机器学习中至关重要，无处不在。

五、张量 | Tensor

张量有很多种定义的方式，这里只讨论人工智能领域里的概念。

在人工智能领域，定义比较简单，TensorFlow是这么定义的：

A tensor is a generalization of vectors and matrices to potentially higher dimensions.

简单翻译过来就是：张量是多维数组，目的是把向量、矩阵推向更高的维度。

• 几何代数中定义的张量，是基于向量和矩阵的推广。
• 
  
• 标量，可以视为零阶张量
• 向量，可以视为一阶张量
• 矩阵，可以视为二阶张量
• 
  

• 图片以矩阵形态表示：将一张彩色图片表示成一个H x W x C 的三阶张量，其中H是高，W是宽，C通常取3，表示彩色图3个颜色通道。
• 
  
• 在这个例子的基础上，将这一定义继续扩展，即：用四阶张量（样本，高度，宽度，通道）表示一个包含多张图片的数据集，其中，样本表示图片在数据集中的编号。
• 
  
• 用五阶张量（样本，帧速，高度，宽度，通道）表示视频。
• 
  

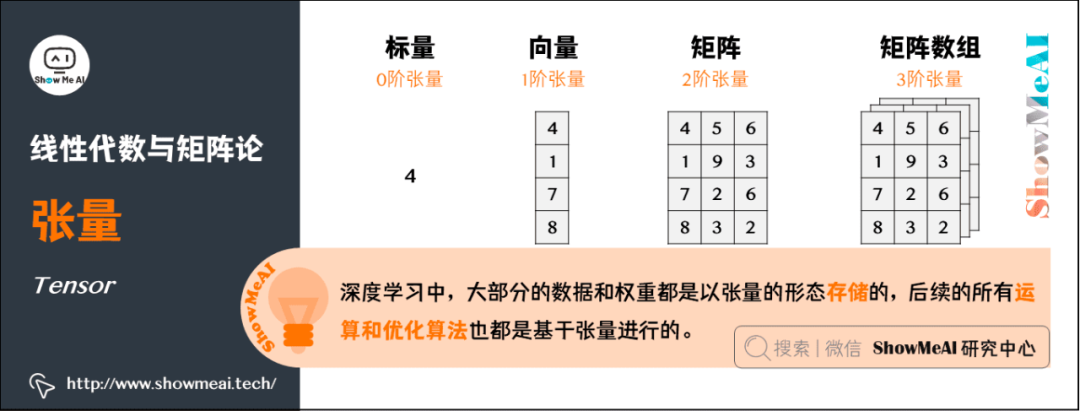
AI中的应用：张量是深度学习中一个非常重要的概念，大部分的数据和权重都是以张量的形态存储的，后续的所有运算和优化算法也都是基于张量进行的。

推荐阅读：（卷积神经网络）https://zhouyifan.net/2022/07/11/DLS-note-10/

六、常用的距离度量

在机器学习里，大部分运算都是基于向量的，一份数据集包含n个特征字段，那每一条样本就可以表示为n维的向量，通过计算两个样本对应向量之间的距离值大小，有些场景下能反映出这两个样本的相似程度。还有一些算法，像 KNN 和 K-means，非常依赖距离度量。

设有两个 n 维变量：

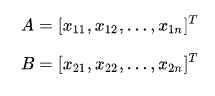
一些常用的距离公式定义如下：

七、余弦相似度（Cosine Similarity）

余弦相似性计算是一种用于衡量两个向量之间角度差异的算法，可以用于计算文本、音乐、图片等相似度。它的原理是，将每个向量看作是n维空间中的一个点，然后计算这两个向量之间的夹角余弦值，最后得到一个介于-1到1之间的值，表示两个向量之间的相似度。

详细计算过程如下：

1. 首先将每个向量表示为n维空间中的一个点，其中n为向量的维度。
2. 计算两个向量之间的夹角余弦值，公式为：cos(θ) = (A·B)/(|A||B|)其中，A和B分别表示两个向量，θ表示它们之间的夹角，A·B表示向量的点积，|A|和|B|分别表示两个向量的模（即向量的长度）。
3. 将夹角余弦值映射到[0,1]范围内，得到两个向量之间的相似度。

下面是详细的计算公式：

假设有两个向量u=(x1,y1,z1)和v=(x2,y2,z2)，它们的夹角余弦值可以使用以下公式计算：

cos(θ) = (x1x2 + y1y2 + z1z2)/(sqrt((x1^2 + y1^2 + z1^2)(x2^2 + y2^2 + z2^2)))

其中，θ表示两个向量之间的夹角，(x1,y1,z1)和(x2,y2,z2)分别是两个向量的坐标。

最后，将夹角余弦值映射到[0,1]范围内，得到两个向量之间的相似度，可以使用以下公式：

similarity = (1 + cos(θ))/2

其中，similarity表示两个向量之间的相似度，余弦相似度的取值范围为-1到1之间，其中-1表示两个向量完全相反，0表示两个向量没有相关性，1表示两个向量相同或方向一致。

同理，

两个n维向量a和b，它们的点积可以表示为：a·b=a1b1+a2b2+...+anbn

n维向量a的模长 |a| = √(x1^2 + x2^2 + ... + xn^2)

空间向量有三个坐标轴，即x、y、z。空间向量的大小也叫做向量的模，表示为|a|，模就是起点与终点的距离

对于两个向量a和b，它们的点积可以表示为：a·b=|a||b|cosθ，其中θ是两个向量的夹角

• 余弦相似度的取值范围为 [-1, 1]，可以用来衡量两个向量方向的差异：
• 
  
• 夹角余弦越大，表示两个向量的夹角越小；
• 当两个向量的方向重合时，夹角余弦取最大值 1；
• 当两个向量的方向完全相反时，夹角余弦取最小值 -1 。
• 
  

机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下：

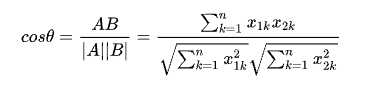
夹角余弦的Python实现：

import numpy as np
vector1 = np.array([1,2,3])
vector2 = np.array([4,5,6])
cos_sim = np.dot(vector1, vector2)/(np.linalg.norm(vector1)*np.linalg.norm(vector2))
print("余弦相似度为", cos_sim)

以上数学基础知识为AI领域常见且非常基础的理论知识，需要大家熟练掌握并运用到实际项目中。

文章来自于微信公众号 “ 威生活”，作者 “ Lion 教授”