【新智元导读】小孩子都会的脑筋急转弯推理题，GPT-4和Claude 3做不出？国外一位开发者小哥坚称这一观点，认为GPT模型在训练集外毫无推理能力，无法实现AGI，甚至悬赏1万美元，发起比赛。然而，他当天就被光速打脸了！网友用高能的prompt，让GPT-4和Claude 3几乎达到百分百的正确率。

ChatGPT，再一次打破人们对它的成见！

它用自己的优秀表现证明了，很多时候自己看似失败的表现，只是因为人类不会正确地prompt而已。

这位名叫Taelin的程序员、初创公司Higher Order的创始人表示，下面这个脑筋急转弯，大多数孩子都能在一分钟内解决，然而所有的AI却都惨遭失败。

这也就成了他给GPT「判死刑」的一个铁证——

GPT模型在训练集之外，没有任何推理能力。GPT永远无法实现AGI。7万亿肯定是白烧的，是时候寻找新的算法了。

为此，他向公众社区发出了一项挑战，任何能用LLM解决这个难题的人，将获得10000美元的奖金。

然而——他！被！打！脸！了！

两天后，一位网友仅通过提示，就让模型解决这道问题时达到了接近100%的成功率。

Taelin迅速「滑跪」，发布声明承认：我最初的主张是错误的。

我怀疑GPT架构是否能解决某些问题，毫无疑问，它可以解决。

并且，他如约给出了10000美元奖金。

沃顿商学院教授Ethan Mollick转发了他的帖子，评论道——

「我们经常能看到这种现象：很多时候我们一个问题LLM无法解决，只有人类能解决，但其实LLM只是需要更好的提示而已。」

大赛始末

Taelin小哥用来考验大模型的A::B问题，题干如下——

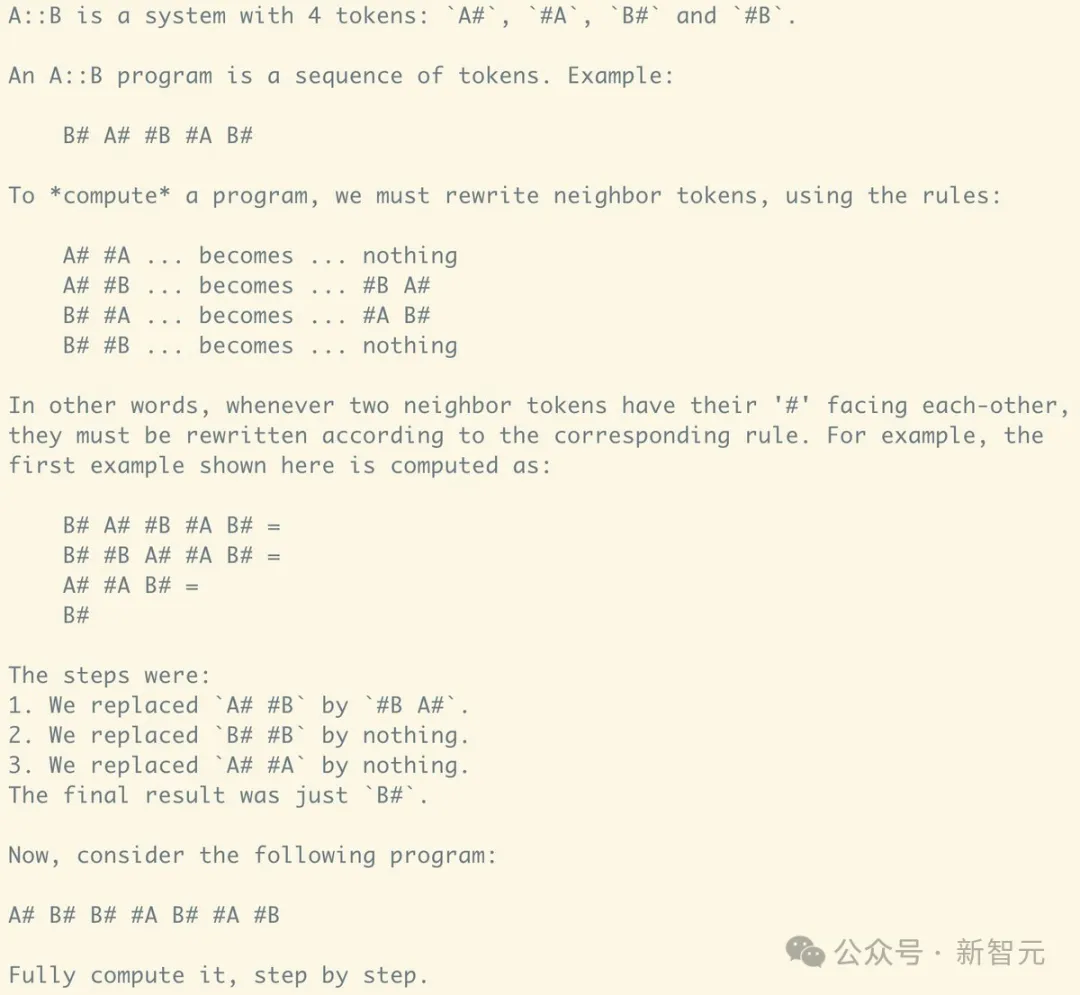
A::B是一个包含有4个token的系统：A#、#A、B#和#B。

A::B程序是一个token序列，例如：「B# A# #В #А В#」。

要计算一个程序，我们必须使用规则重写相邻token：

「A# #A」变成「无」

「A# # B」变成「#B A#」

「B# #A」变成「#A B#」

「B# #B」变成「无」

换句话说，只要两个相邻token符的「#」相向，就必须根据相应的规则进行改写。

例如，第一个例子的计算方法是：

B# A# #B #A B#

= B# #B A# #A B#

= A# #A B#

= B#

步骤如下：

1. 将「A# #B」替换为「#B A#」。

2. 将「#B A#」替换「B# #B」。

3. 将「A# #A」替换为「无」。

最后的结果只有「B#」。

现在，请看下面这个程序：「A# B# B# #A B# #A #B」。

一步一步完成计算。

对此，他是这样解释的——「GPT永远不会解决A::B问题」，因为：

1. GPT无法真正学习到训练集之外的新问题；

2. GPT无法进行长期的逻辑推理，不管这个推理过程看起来多么简单。

而这两点是发明新科学的必要条件。

毕竟，解决某些数学问题可能需要数年时间。

如果连一个15岁的孩子在智力任务上都比不过，那么就不可能证明黎曼假设。

1万刀的挑战长啥样？

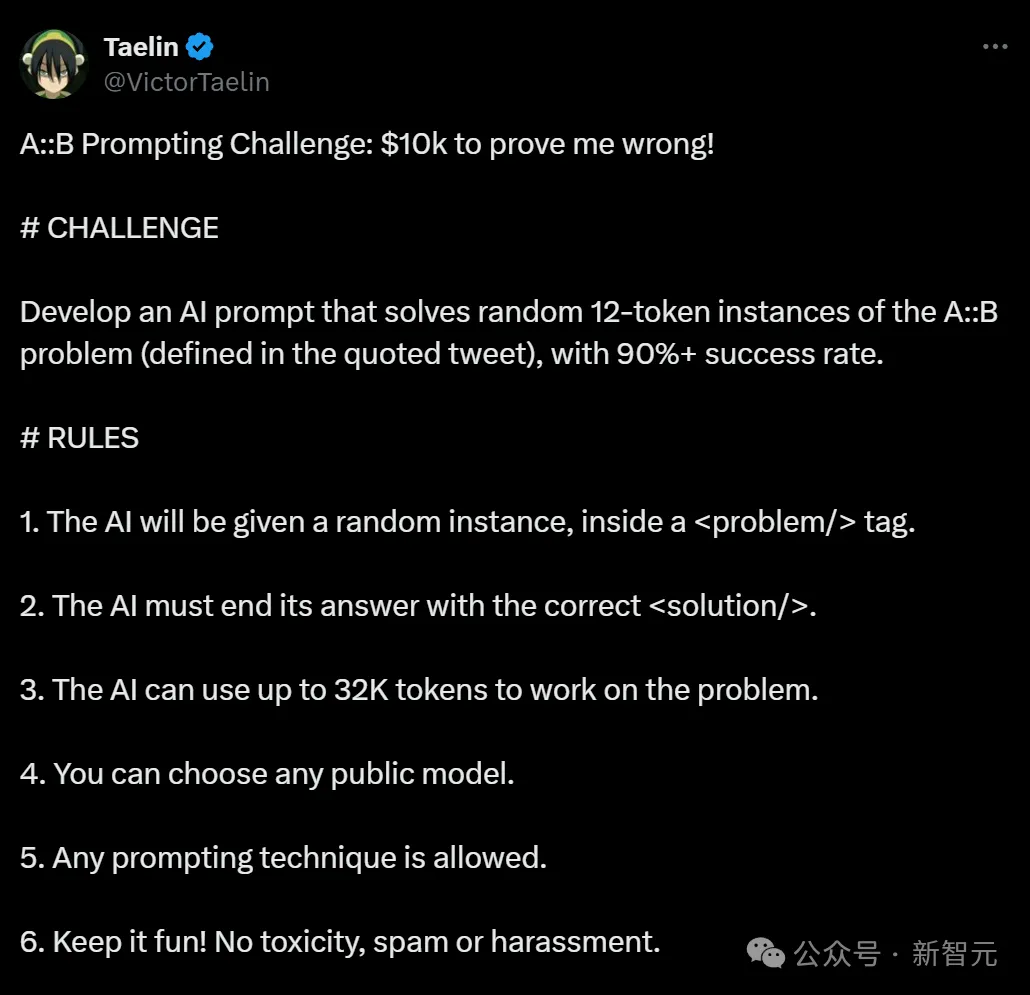
小哥给大家的挑战就是，必须开发出一个AI提示，能够解决随机的12-token实例的A::B问题，并且成功率超过90%。

挑战地址：https://gist.github.com/VictorTaelin/8ec1d8a0a3c87af31c25224a1f7e31ec

规则

1. AI将接受一个<problem/>来解决

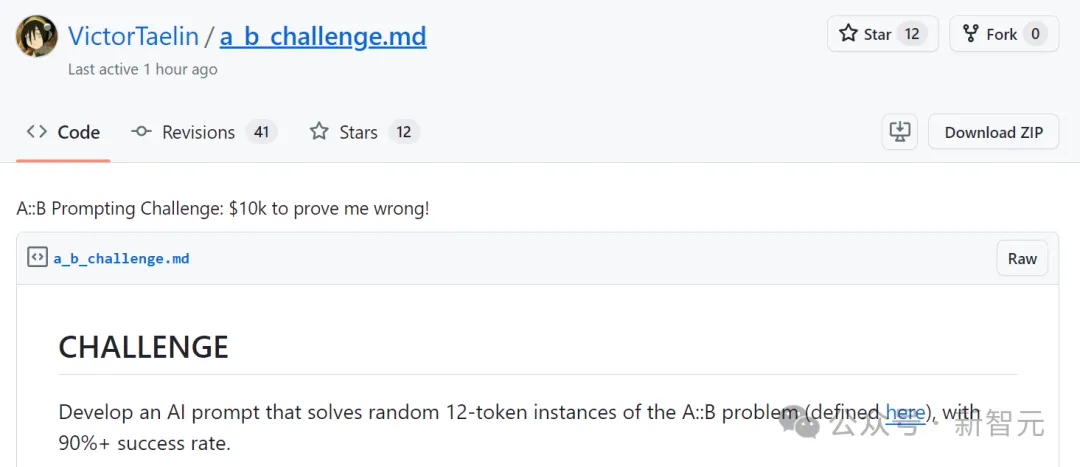
XML标签中的提示将作为系统提示用于解题。例如：

<problem>A# B# #B A# A# #B #B A# A# #B A# A#</problem>

2. AI必须在答案中以<solution/>结束

答案必须在AI的回答中（一次推理调用内）直接给出，格式为纯文本（不是代码），并放在XML标签中。例如：

... work space ...
... work space ...
... work space ...
... work space ...
<solution>#B #B #B A# A# A# A# A# A# A#</solution>

3. AI答案最多可包含32K token

这个token数，已经足够提供充足的空间，让AI逐步解决问题和纠错了。

4. 你可以选择任何一个公开的GPT模型

任何基于GPT（Transformer）架构的公开模型都可以，条件是它完全由注意力机制、正向传播等来生成答案。

不允许使用其他架构，如SAT求解器。底层架构不明确的专有模型，也不允许使用。

作者推荐使用的是gpt-4-0314、gpt-4-turbo-preview或claude-3-opus-20240229，设置温度为0.0（temperature=0.0）。开源模型亦可。但简直对问题进行微调或训练。

不允许访问互联网或执行代码。答案必须在单次推理调用中自成一体。

而且，需要格外注意模型的输出限制。12-token的实例可能需要36步才解决，如果超出限制，导致输出中没有答案，也视为无效。

5. 你的提示可以包含任何内容，最多8K token

允许使用任何提示技术。你可以要求AI step-by-step，使用上下文暂存器，检查错误，使用锚点。

允许提供论文、代码、尽可能多的示例。

甚至允许向AI提供金钱和情感上的奖励，或者对它威胁。

总之，只要在8K token以内，什么都可以。

一天内，有人成功揭榜

大赛开始后，才短短几小时内，开发者们就提交了众多解决方案。

然而，这些方案几乎都毫无例外地失败了，成功率只勉强达到10%。

小哥感觉，自己差不多稳了。

谁料想，就在这时，两位网友提交了一个令人印象深刻的解决方案。

在他们精心设计的提示引导下，Claude-3 Opus展现出了惊人的能力——

它不仅能从少数示例中归纳出任意随机情况，还能严格遵守规则进行长期计算，并且错误率几乎为零。

Taelin测试后惊讶地发现，Claude-3 Opus居然取得了56%的惊人成功率！

随后，先后有5位参赛者，分别用Opus和GPT-4达到了相似的成功率，甚至GPT-3.5都取得了不错的成绩。

到了当天深夜，竟然有网友提交了满分答卷！

futuristfrog发布了一条推文，声称仅通过精心设计的提示就实现了近乎100%的成功率。

事实证明，他的确做到了。在小哥的首次测试中，他的方案在50次尝试中成功了47次，因此赢得了奖金，圆满完成了这一挑战。

讨论激烈

问题一出，便引发了激烈的讨论。

有网友表示自己没做任何修改，GPT-4就做了出来。

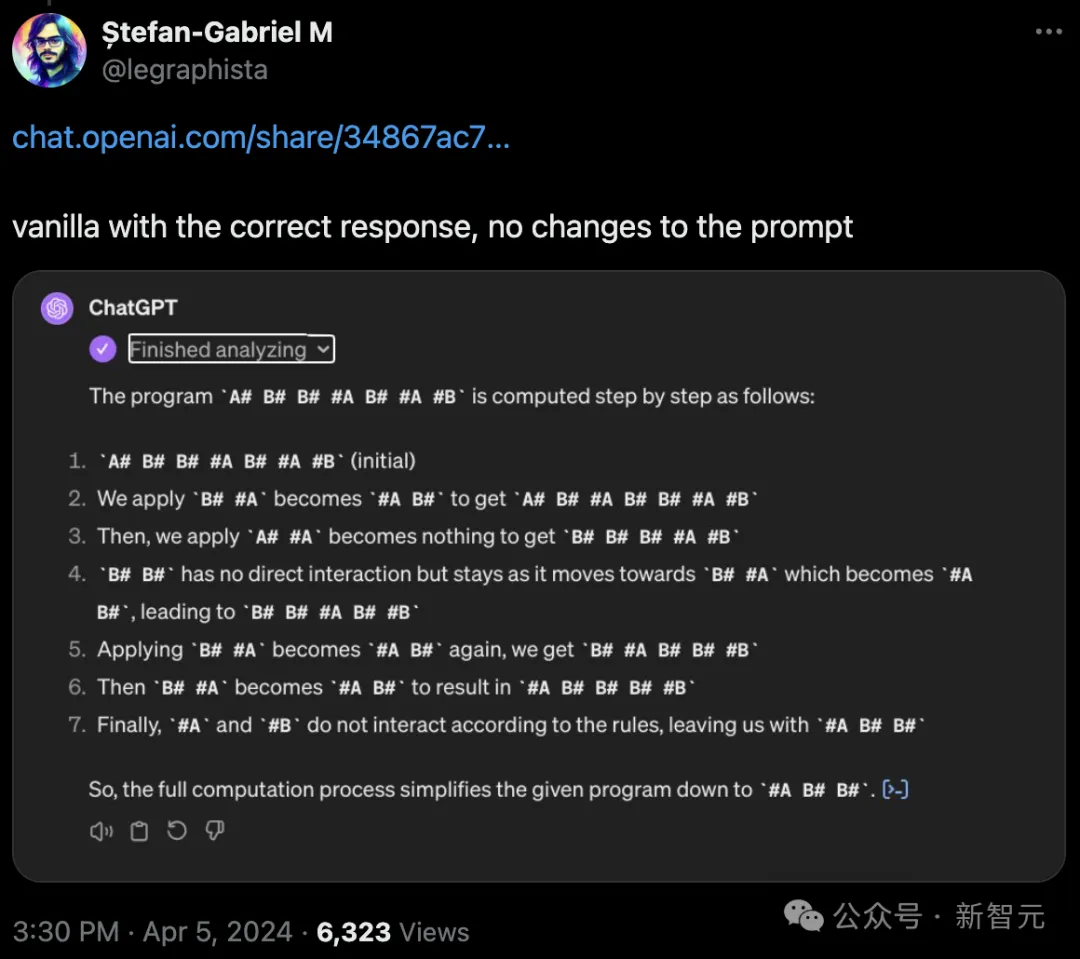
但很快就被其他网友指出了错误。

高赞回答表示，如果让GPT-4编写程序，这道题实际上是非常容易的。

但很明显，你不能说LLM + Python就能得到AGI。

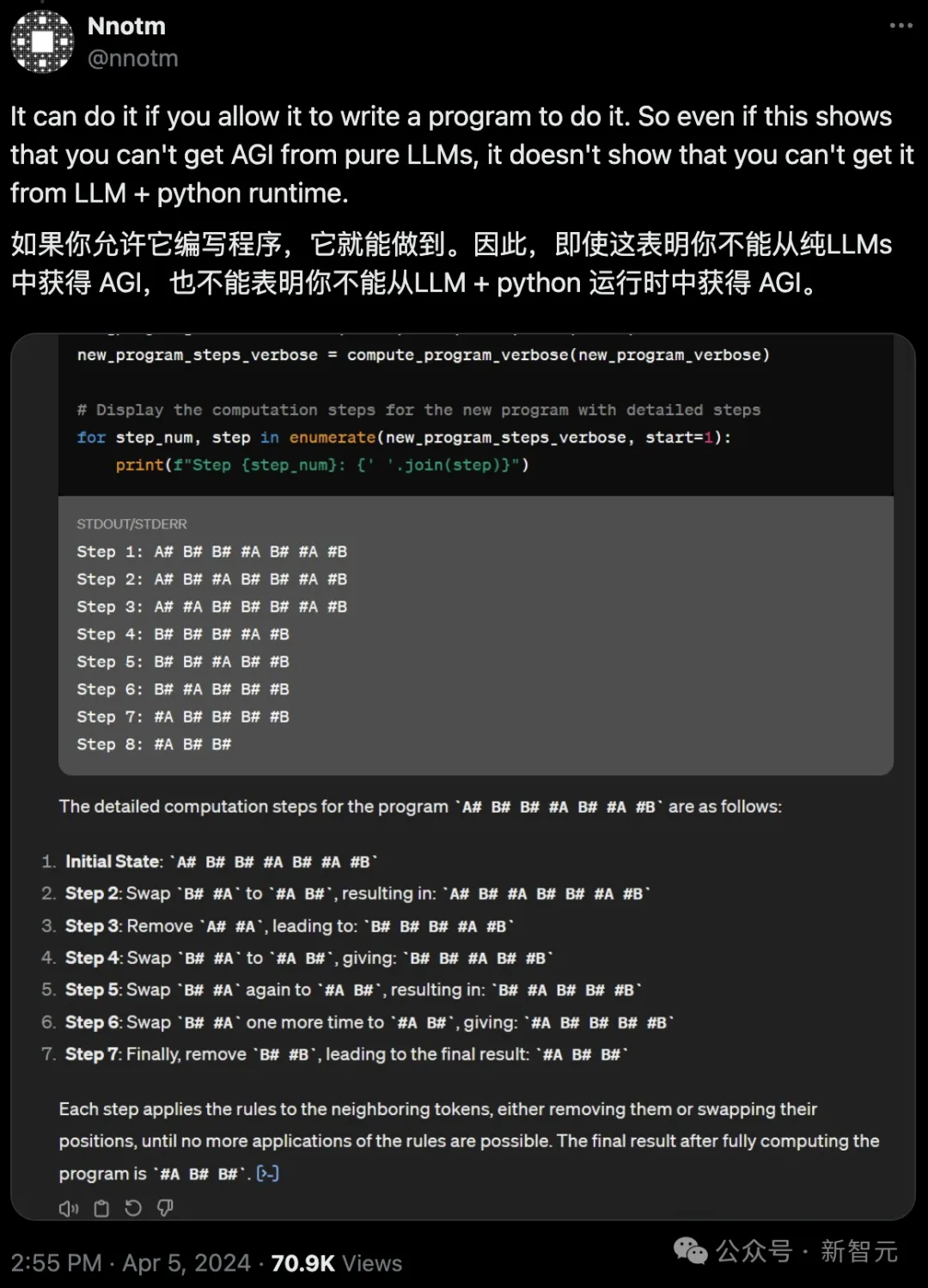
与此同时，各路网友也纷纷开始提交自己做出的答案。

但也有不少人认为，作者出的这道题，很有问题。

Eric (e/ass)表示，正如Karpathy多次指出的，token化问题是导致序列操作成功或失败的关键因素。

如果在token化过程中出现了问题，那么即使是更简单的字符串操作也无法顺利完成。

相比之下，token化处理得较好的字符串（例如连续的两个字母）就很容易进行操作。

当然，这并不意味着GPT在管理规则排列的token的空间布局方面没有本质的问题。

实际上，它在这方面的表现并不出色，而且将其分解为字节也并没有太大帮助，因为这会使需要移动的数据单元占用更多空间。

与人类能够进行动态分块处理不同，目前的LLM还没有找到有效的解决方案。

你提到的逻辑问题可能确实存在，但这个例子并没有证明GPT存在无法克服的根本性限制。

或许随着技术的进步会诞生更强的模型，但这并不意味着如今的Transformer在进行基本推理方面存在明显的短板。

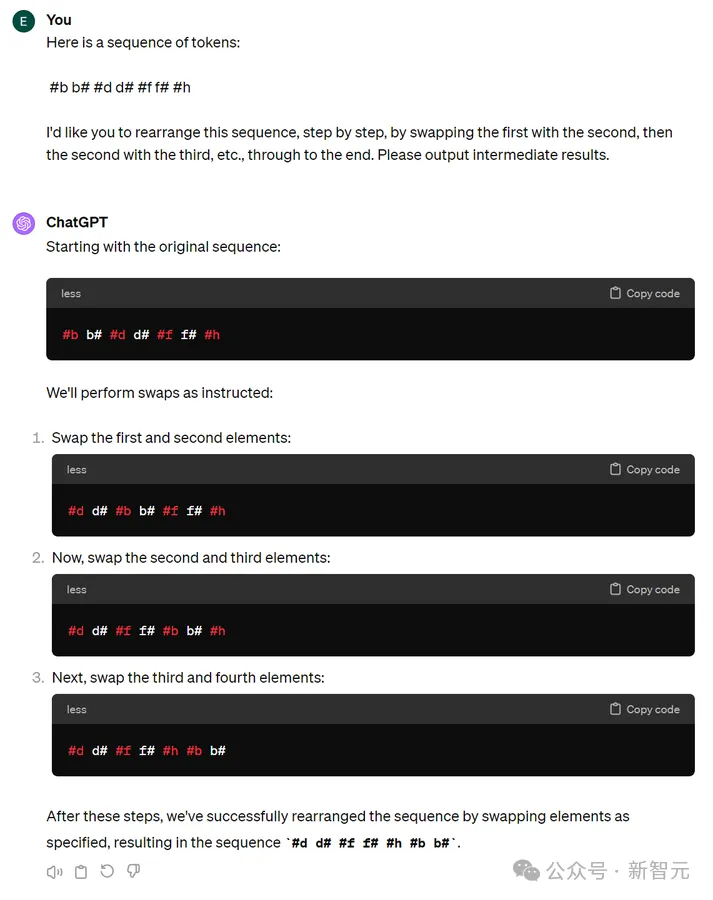
Edgars Nemše也认为，这不是因为GPT推理能力不行，而是被自己的「观察」方式限制住了。

作者解释

最后，为了让大家能更好地理解这个挑战，我们来看一看Taelin自己的详细解释。

1. 这个问题并非由token化引起的。即便是每个符号分配一个token，GPT-4、Opus等模型仍然无法解决这类问题。即使是基于字节的GPT模型也同样失败。不要总是将问题归咎于token化。

2. GPT无法解决这类问题的根本原因在于，它们缺乏进行持续逻辑推理的能力。简而言之，任何超出训练集范围、哪怕只需一丁点逻辑推理的「新问题」，GPT都无法应对。这正是我们想要证明的。

3. 强大如GPT-4或Opus之类的模型，其实质上是在其权重中「演化出了一位电路设计师」。但是，注意力机制作为一种计算模型的固定性，使得这种演化的电路无法展现足够的灵活性。这就像AGI试图在其中成长，但由于计算和通信的限制而无法做到。相比之下，人类的大脑始终在经历着突触可塑性变化。

4. 一个冷知识是，当前AI热潮的很大一部分原因是人类不善于理解规模的巨大。一旦你记住了整个互联网的内容，你看起来会非常聪明。

5. 尽管如此，GPT依然展现出了强大的能力。它们解决了许多现实世界的问题，将普通开发者的能力提升了数百倍，并以此加速了人类进步的步伐。我相信通用人工智能的到来已经近在咫尺。但它不会是GPT，也不会是任何基于梯度下降的形式。

6. 我的看法可能完全错误。毕竟，我只是互联网上的一名普通人，而且经常犯错。

参考资料：

https://twitter.com/VictorTaelin/status/1776677635491344744

文章来自微信公众号“新智元”，作者:新智元