首位超越国际奥林匹克竞赛金牌得主的AI，刚刚诞生了！

印度理工学院海得拉巴分校、图宾根AI中心、剑桥大学的研究者发现——

通过「吴方法」，可以让AI变成和人类数学奥赛银牌得主同样的水平，而「AI数学大师」AlphaGeometry，则直接超越了IMO金牌得主。

吴方法，是吴文俊在1970年代提出的开创性算法。

经过改进后，它变得非常强大，可以解决国际数学奥林匹克竞赛30个问题中的27个！直接秒杀人类。

相比之下，之前的AlphaGeometry，仅能解决25个。

论文地址：https://arxiv.org/abs/2404.06405

项目地址：https://huggingface.co/datasets/bethgelab/simplegeometry

之前曾有人估计，到2026年代，AI才能达到IMO人类金牌得主的水平。而如今，这个时间表再次被打破了。

AI做IMO奥数题，有新SOTA了

证明几何定理是视觉推理的重要表现，它融合了直觉和逻辑思维。

因此，自动化证明奥林匹克级别的几何题目，代表着人类级自动推理的一个重要里程碑。

此前推出的AlphaGeometry，是一个通过1亿个合成样本训练的神经符号模型，代表了一个重大的突破。

论文地址：https://www.nature.com/articles/s41586-023-06747-5

它成功解决了国际数学奥林匹克（IMO）30个问题中的25个，而传统的基于吴方法的系统，仅能解决10个。

但这一次，研究者们重新评估了AlphaGeometry引入的IMO-AG-30挑战，有了新的发现——

吴方法异常强大！

仅靠吴方法，就能解决15个问题，其中一些问题是靠其他方法根本无法解决的。

而这就带来了两个关键发现：

1. 通过将「吴方法」和经典的演绎数据库（DD）以及角度、比率和距离追踪（AR）的合成方法相结合，仅使用一台配备CPU的笔记本，在每个问题的5分钟限时内，就能解决30个问题中的21个。

这种经典组合方法（Wu&DD+AR）仅比AlphaGeometry少解决了4个问题，并建立了第一个完全基于符号的基准，其性能足以与国际数学奥林匹克（IMO）银牌得主媲美。

2. 吴方法还解决了AlphaGeometry未能解决的5个问题中的2个。

因此，现在IMO-AG-30有新的SOTA了！

通过将AlphaGeometry与吴方法结合产生的新AI，直接解决了30个问题中的27个，一举超越IMO金牌得主，成为世上首个达此成就的AI。

欧氏几何，AI推理能力的试金石

如何测试AI的推理能力强不强？欧几里得几何就是一个很好的标准。

因为，欧几里得几何已经被有限地公理化了，而且这么多年来，有许多非常适合自动定理证明的欧几里得几何证明系统被提了出来。

此外证明的搜索可以通过图形表示、概率验证，或是使用人类设计的启发式方法，来对角度、面积和距离进行大量推理引导。

国际数学奥林匹克中，这些方法被参赛者戏称为「三角破解」和「重心破解」。

还有一件有趣的事，就是这个领域的缺陷——它需要定义特定的证明系统来指定问题，缺乏训练数据，问题时常涉及复杂的退化情况。

这些困难非常棘手，由此坊间有这样一句戏言——「几何问题永远不会解决退化问题。」

在几何自动推理领域，可以将方法分为代数方法和合成方法。

演绎数据库（DD）这个合成方法就颇受关注。

它会模仿人类的证明技巧，通过将定理证明视为依据一组几何公理进行的逐步搜索问题，从而生成易于理解的证明。

比如，DD会采用一组固定的、由专家策划的几何规则，这些规则会不断地应用到初始的几何配置上，直至系统达到一个状态，即用现有规则无法推导出新的事实为止。

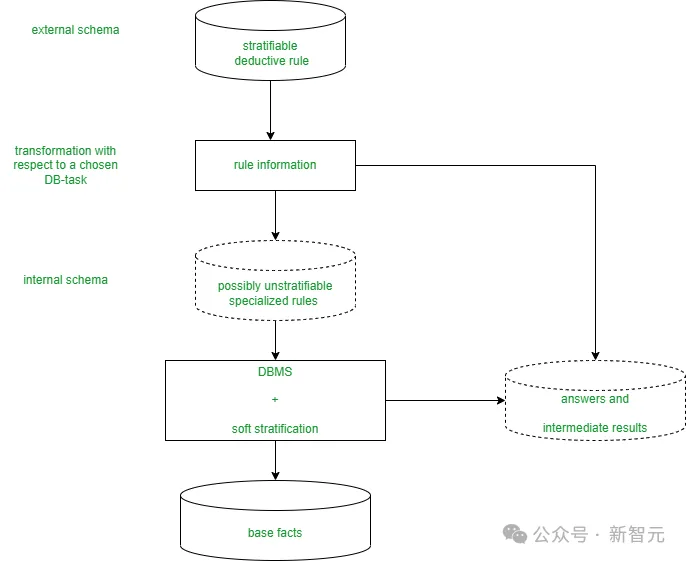
而神经符号证明器AlphaGeometry在这一领域取得了突破性的进展。

在DD的基础上，它增加了新的规则，用于进行角度、比率和距离的追踪（AR），并通过大模型（DD+AR+LLM-构造）提出的构建方法，进一步增强了由此生成的符号引擎。该模型是基于1亿个合成证明训练

的。

而吴方法和Gröbner基方法之类的代数方法，能够将几何假设，转换成多项式系统，来验证结论。

这些方法已被证实，能够有效处理广泛的几何问题。

其中，对于所有假设和结论都能用代数方程表示的问题，吴方法都能处理，并且还能自动产生非退化条件。

而这就表明，吴方法不仅适用于平面几何问题，也适用于固体和更高维的几何问题。

5秒解决14个问题

今年1月，谷歌DeepMind团队同时推出了新的基准测试IMO-AG-30。

这是团队从2000年至2022年间竞赛题中，筛选出30道经典几何问题组成的测试集，目的是为了展示AlphaGeometry的性能。

基准中，问题的解决数量与IMO选手的平均解题数量相对应。

如下图，灰色水平线所示，铜牌、银牌和金牌得主平均分别解决了19.3个、22.9个和25.9个问题。

所有参赛者平均解题数为15.2。

IMO-AG-30收集的具体问题集在图1（B）的左列中有所列出。

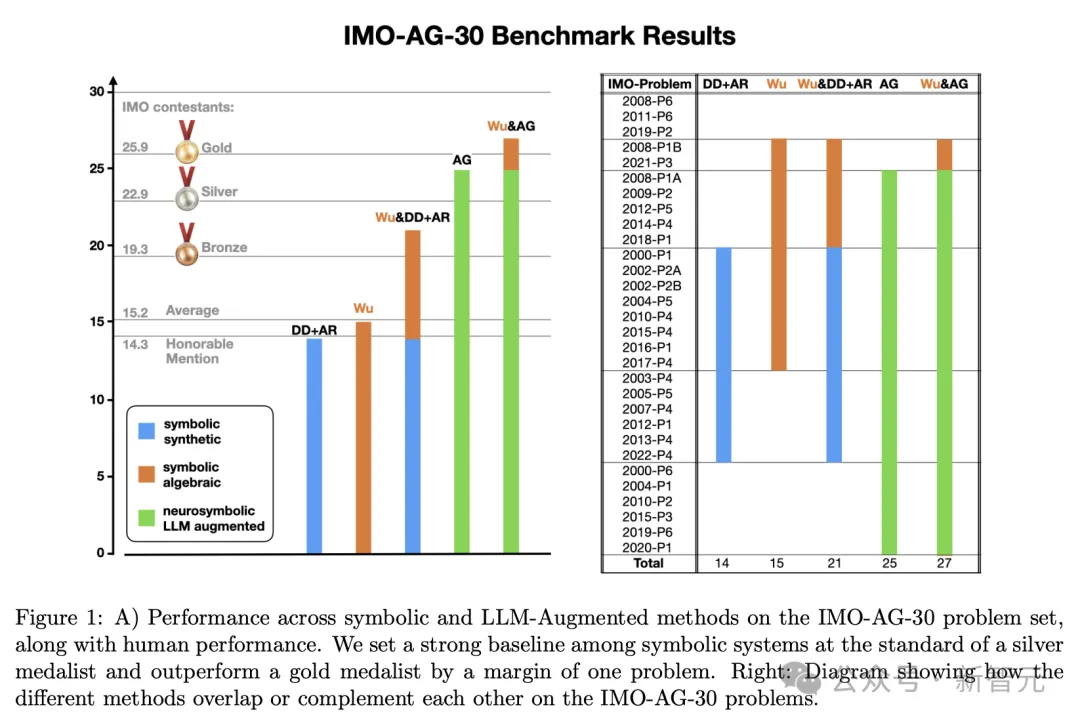
（A）在IMO-AG-30问题集上，符号系统和增强型大模型（LLM-Augmented）的表现，以及与人类表现的对比

（B）展示了不同方法在解决IMO-AG-30问题集时的情况

实验

研究人员根据Trinh等人提供的基线和数据集，使用IMO-AG-30基准进行性能评估。

他们通过JGEX软件手动将IMO-AG-30问题转换成兼容格式，并重新实现了吴方法。

同时，研究者也从AlphaGeometry代码库中成功重现了必要的DD+AR基线。

经过手动验证了自己翻译的几个问题，团队确认JGEX生成的假设和结论方程是正确的。

吴方法解决了AlphaGeometry未能解决的两个问题，方案插图如下所示。

2008-P1B（JGEX）：

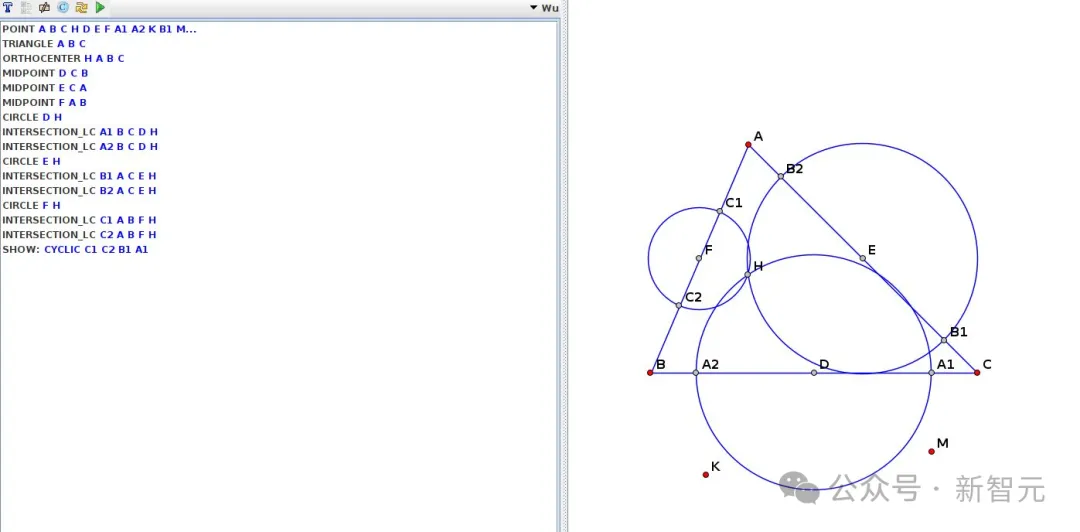
生成的答案：

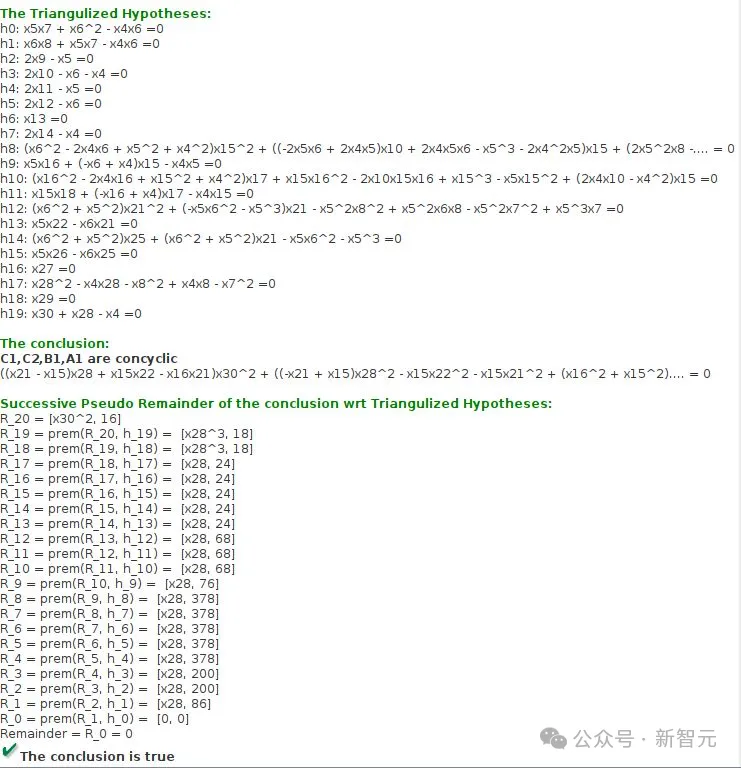
2021-P3（JGEX）：

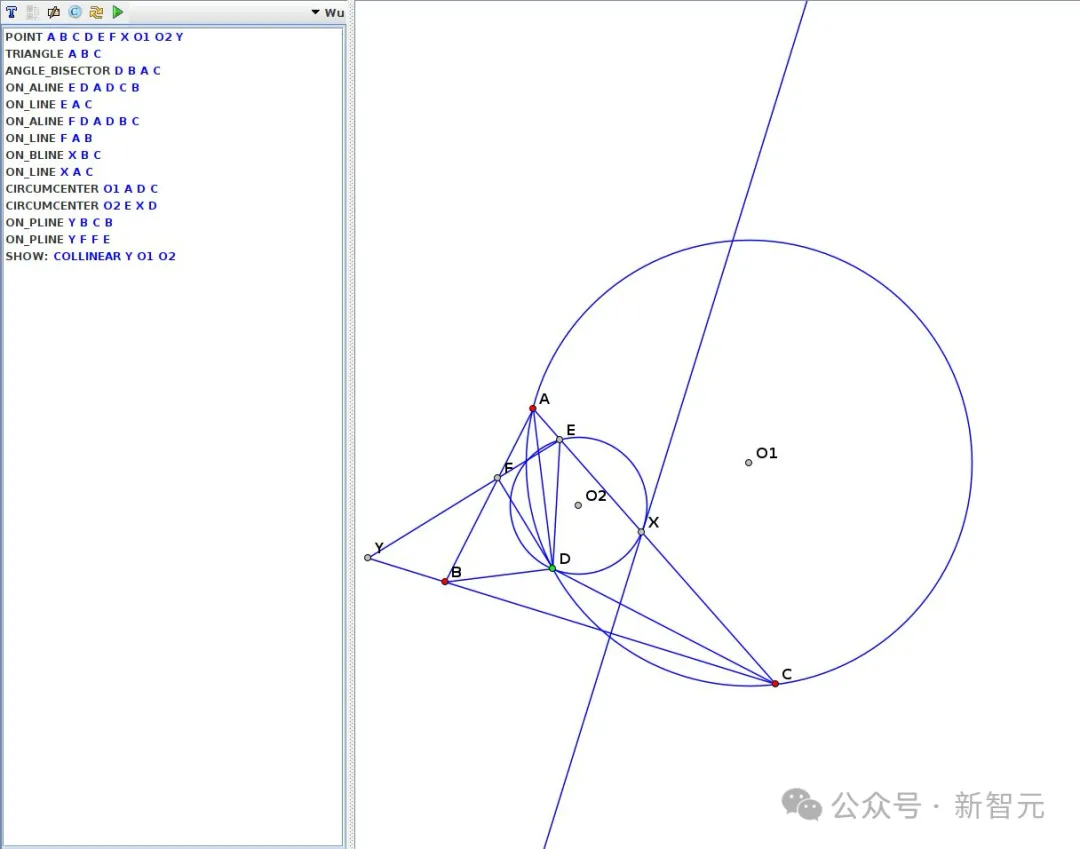
生成的答案：

结果

研究结果与的先前结果，已经在图1中进行了展示。

图1（A）比较了解决问题的数量，图1（B）展示了各种方法解决的具体问题，以此可视化不同方法之间的重叠或互补性。

具体来说，研究人员将吴方法与DD+AR结合，创建了一个新的符号性能基准（Wu&DD+AR），该基准比所有传统方法多解决了6个问题。

这种组合解决了IMO-AG-30问题中的21个，与图2中未经微调（仅FT-9M）的AlphaGeometry的表现相匹配。

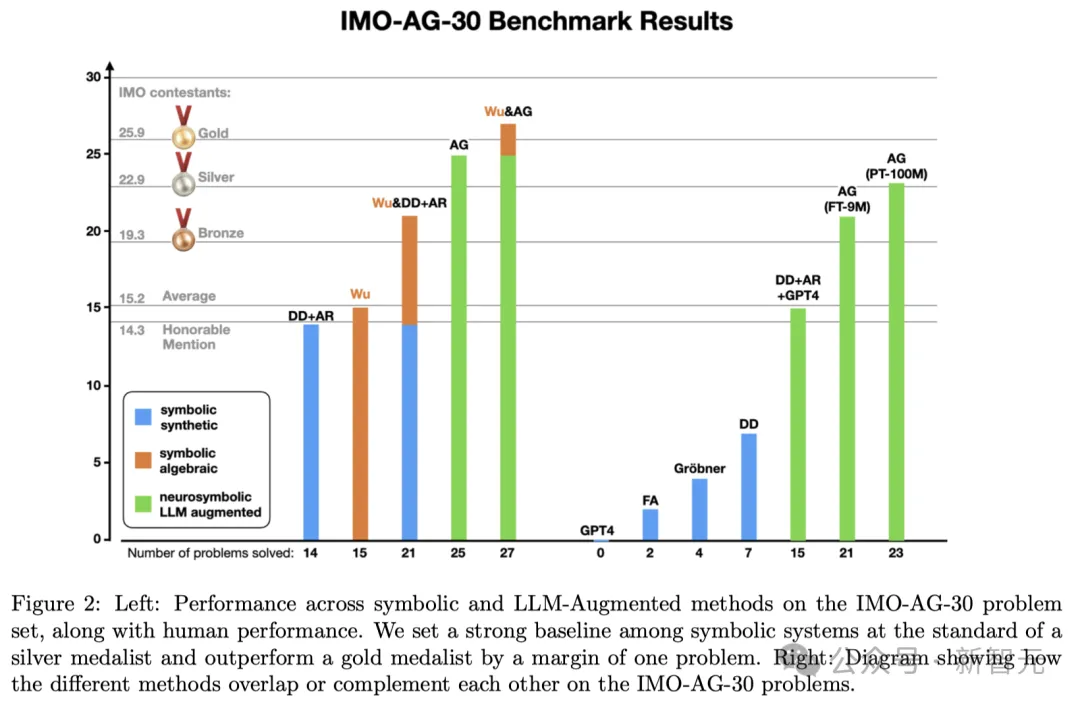
（A）展示了在IMO-AG-30问题集上，符号方法和LLM增强（LLM-Augmented）方法的表现，以及与人类表现的对比

（B）展示了不同方法在IMO-AG-30问题上的表现

吴方法在非常低的计算需求下实现了这一表现。

在一台装有AMD Ryzen 7 5800H处理器和16 GB RAM的笔记本上，研究人员在5秒内解决了15个问题中的14个，其中一个问题（2015 P4）需要耗时3分钟。

在实验中，吴方法要么几乎立即解决问题，要么在5分钟内使笔记本内存耗尽。

值得一提的是，研究者通过吴方法解决的15个问题中的2个（2021 P3, 2008 P1B），原本是AlphaGeometry难以解决的5个问题之中的2个。

因此，通过简单地将Wu的方法与AlphaGeometry结合，实现了在IMO-AG-30基准上解决了27个问题，这一成就在图1的绿色/橙色条形（Wu&AG）中有所展示。

代数方法攻克IMO

代数方法，在自动化几何推理中解决IMO几何问题中，蕴藏着巨大的潜力。

这项研究恰恰印证了这一点，吴方法也从过往能够解决10个问题，增加到了15个问题。

而这些问题中，有几个对于目前流行的合成方法，以及增强LLM的方法，也具有非常高的挑战性。

研究者表示，其设立的符号基线，是首个在性能上超越一般IMO参赛者，并接近银牌水平。

此外，AlphaGeomtery和吴方法结合的系统，也是首个在IMO几何问题上超越人类金牌得主的AI系统。

这一成就证明了，代数方法与合成方法在这一领域的互补性。特别是，2008 P1B和2021 P3这两个问题目前仅有吴方法能解决，显示了代数方法的独特价值。

尽管代数方法以其理论保证而著称，但之前因速度慢和难以为人理解而受到质疑。

而最新的研究观察显示，吴方法在多个问题上的效率远超预期，作者认为不应仅因其无法生成人类可读的证明而忽视它。

目前，研究还在进行中，受限于现有实现的不足，包括结构的限制和性能不佳。

研究者相信，传统方法有可能超越AlphaGeometry的证明能力，并希望这份研究能促进这一领域经典计算方法软件的改进。

另一方面，最新方法取得的显著成功表明，尽管IMO几何问题对人类具有挑战性，但可能并未充分挑战现代计算求解器的极限。

解题的成功更多依赖于，重复使用人定义的启发式方法和有限的构造，而不是深入探索复杂的组合可能性。

这与国际象棋残局的情况类似，其相对较早就被暴力求解器掌握了。

而研究人员希望这份研究，能激励开发几何领域自动定理证明器的新基准。

参考资料：

https://arxiv.org/abs/2404.06405

文章来自微信公众号“新智元”，作者：新智元编辑部