只要1/200的参数，就能让大模型拥有和GPT-4一样的数学能力？

来自复旦和上海AI实验室的研究团队，刚刚研发出了具有超强数学能力的模型。

它以Llama 3为基础，参数量只有8B，却在奥赛级别的题目上取得了比肩GPT-4的准确率。

这款模型名为MCTSr，是将AlphaGo中用到的蒙特卡洛算法与Llama3结合而成。

它能用少量的数据实现和GPT-4等的相同效果，让网友感叹Q*成真了，小模型在数学上也能做的和GPT-4等著名模型一样好。

就此又有网友表示，MCTSr能用极少的参数实现相同的效果，加上有时候训练收益随规模递减，表明架构才是当前AI的瓶颈，而不是运算。

这样的趋势也让人想起了AI算力霸主英伟达，开始思考规模化是不是不那么重要了，会不会利空老黄呢？

所以，MCTSr具体运用了什么样的方法呢？

将蒙特卡洛引入大模型

MCTSr名字里是MCT，指的就是蒙特卡洛树（Monte Carlo Tree），而Sr则指的是自我完善（Self-Refine）。

蒙特卡洛树又称随机抽样或统计试验方法，是指一种使用重复随机采样生成合成模拟数据的近似方法，谷歌的围棋机器人AlphaGo当中也用到了这种方法。

名字中没有体现的，是蒙特卡洛与大模型的结合，本项目当中使用的是Llama 3-8B，同时MCTSr还引入了自我修正和自我评估的迭代过程。

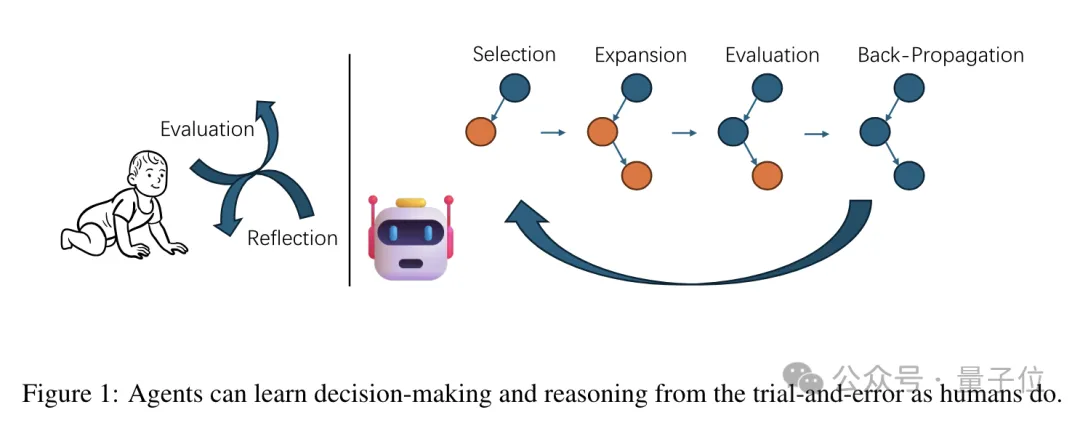
在解答数学问题时，MCTSr中的大模型首先会像正常流程一样生成初步答案（甚至可以是“我不知道”），但并不会直接作为输出。

为了改进这个初始答案，MCTSr算法会对其进行评估和反馈，语言模型会被要求对答案进行评价和批评，分析其中可能存在的问题。

然后大模型基于反馈进行自我修正，产生一个新的答案，这个新版本会纳入搜索树中，成为一个新的子节点。

针对多个子节点，系统会进行评分和奖励采样，计算出该节点的“Q值”（a表示答案节点，Ra表示a的奖励样本集合，|Ra|表示样本数量），可以看出Q值的计算综合考虑了节点在最坏情况和平均情况下的表现。

为了提高评估的可靠性，系统采用了严格的打分标准，并会进行重复采样，同时还采取了禁止模型给出满分等策略。

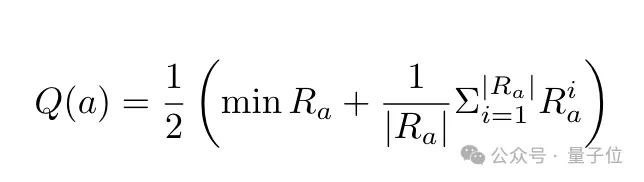
然后基于Q值，MCTSr会使用改进的UCB公式计算每个叶子节点的UCT值，选择UCT值最高的节点进行扩展。

（UCB是一种实现总奖励最大化的方式，UCT是将UCB策略应用于树形搜索问题的一种算法。）

计算UCT值的目的，是为了平衡了节点的平均奖励和访问频率，避免单纯追求高Q值导致的效率下降。

此外，作者修正的UCT计算公式中还引入了动态调整探索系数c，以便在搜索过程中适应不同的问题复杂度，并在探索广度和深度之间做出平衡。

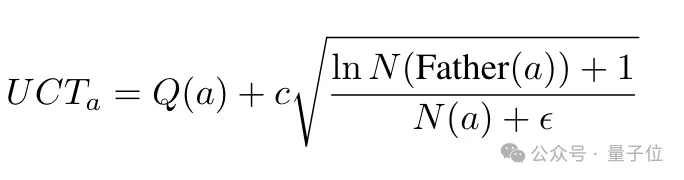
被选中的节点，会通过大模型再次进行自我修正，生成新的答案节点，然后再次进行自我评估并计算Q值。

新的Q值会被并反向传播到其父节点和祖先节点，确保了搜索树中节点的质量评估随着搜索的进行而不断改进。

根据新的Q值和访问次数，各个节点的UCT值也会被重新计算。

接着，上述步骤会被不断重复，直到满足预设的终止条件，此时具有最高Q值的答案节点被视为问题的最优解。

总的来说，通过蒙特卡洛搜索、自我完善与大模型的集合，MCTSr实现了数学问题最优解的生成。

那么，这种方法的实际效果究竟如何呢？

成绩不输GPT-4和Claude-3

在测试当中，作者一共使用了四种模型配置——零样本思维链（CoT），以及1/4/8轮自我优化的MCTSr，其中零样本为对照组。

测试数据集包括MATH的5个level，GSM-8K和GSM-Hard，以及一系列奥赛级别的数据集——AIME、Math Odyssey 和OlympiadBench。

先看简单一些的GSM和MATH。

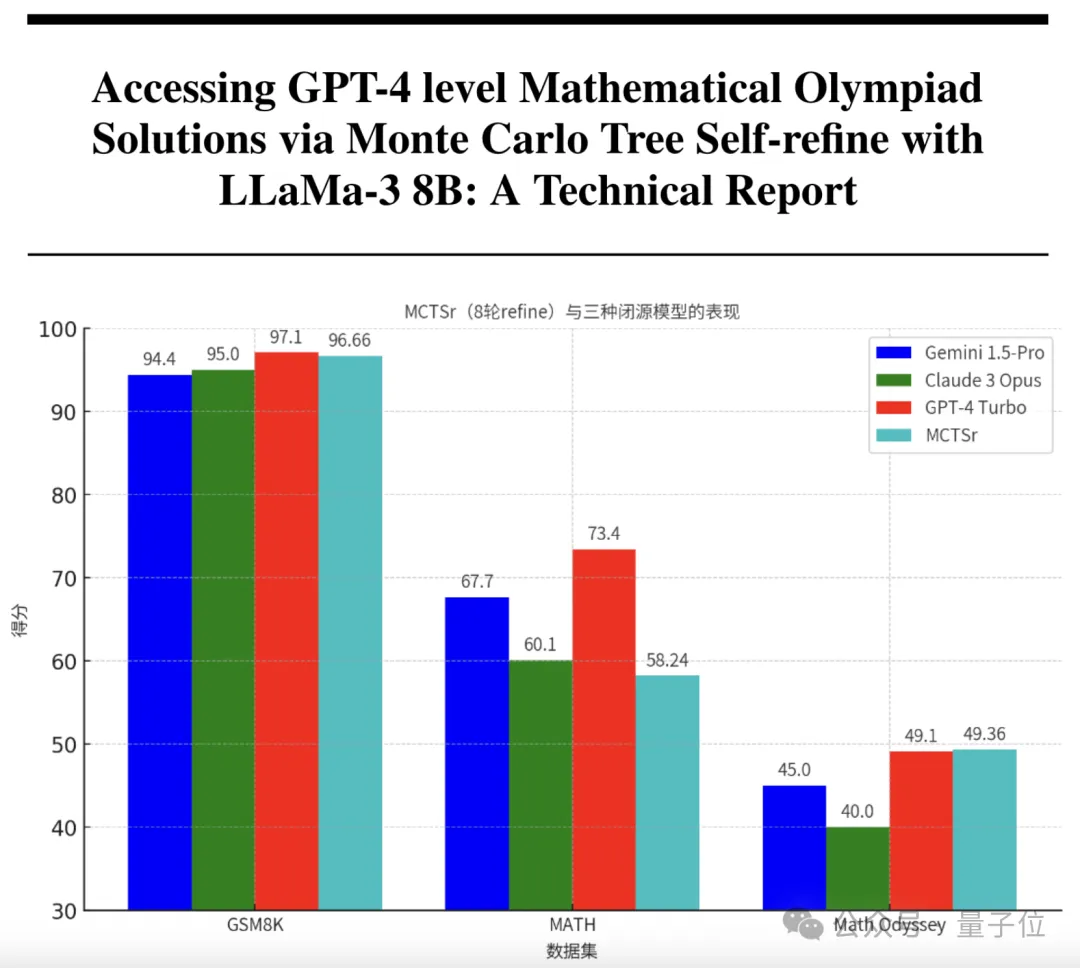
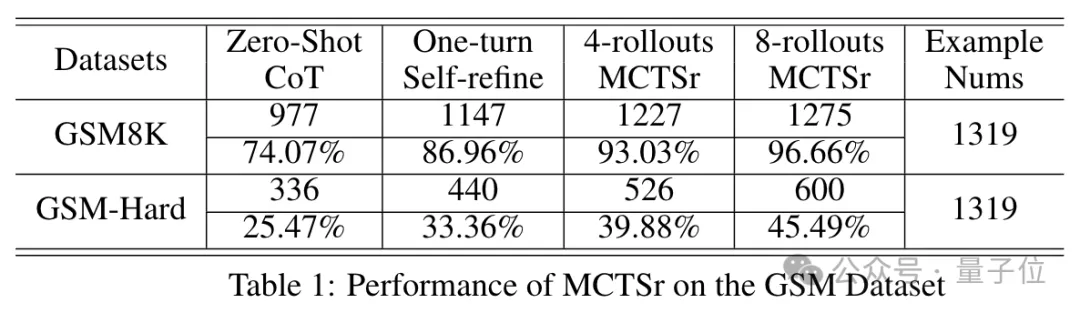
从下表中可以看出，随着自我优化轮数是增多，模型取得的准确率也在增加，经过8轮之后，在GSM-8K上已经达到了96.66%。

而Gemini（1.5Pro，下同）、Claude-3（Opus，下同）、GPT-4（Turbo，下同）的成绩则分别是94.4、95和97.1，可以看出参数只有8B的MCTSr和这些先进模型不相上下。

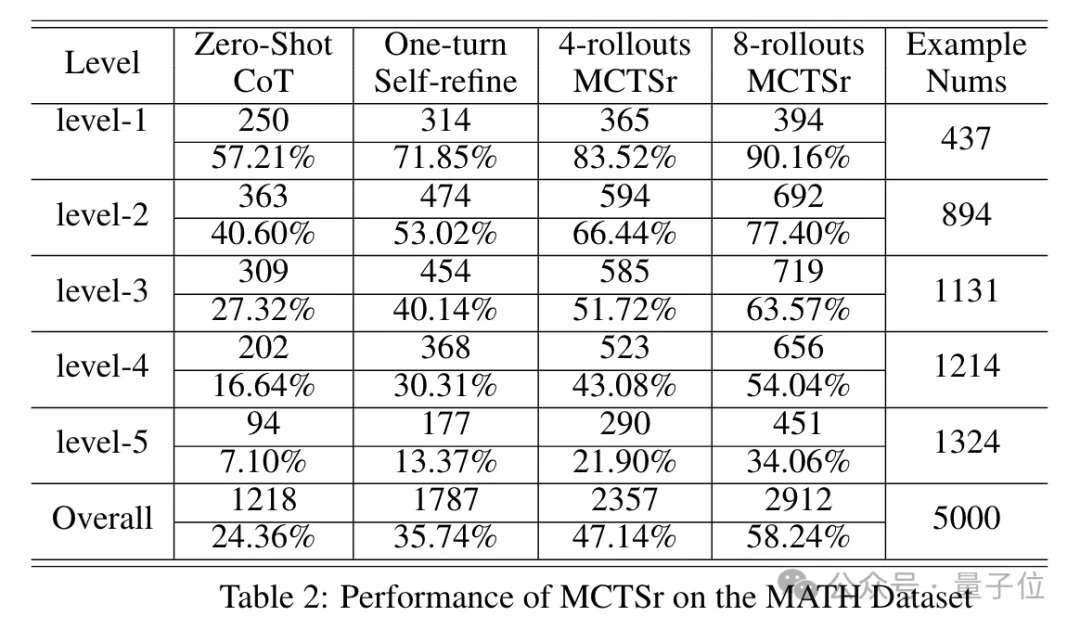
同样在MATH上，无论是整体还是细分的五个难度等级，成绩随优化轮数的变化都呈现出了相同趋势。

特别是在最困难的Level-5上，8轮后的成绩已经接近了对照组的5倍。

在MATH上，Gemini、Claude-3和GPT-4的成绩分别为67.7、60.1和73.4，相比之下MCTSr略逊一筹，但也和Claude比较接近。

在更加困难的奥赛级别题目上，自我优化给MCTSr带来的能力增强也十分显著。

在Math Odyssey上，MCTSr甚至超过了Gemini、Claude-3和GPT-4，三者的成绩分别是45、40和49.1。

同时，在OlympiadBench上，经过8轮优化后，MCTSr的成绩是零样本时的6.2倍。

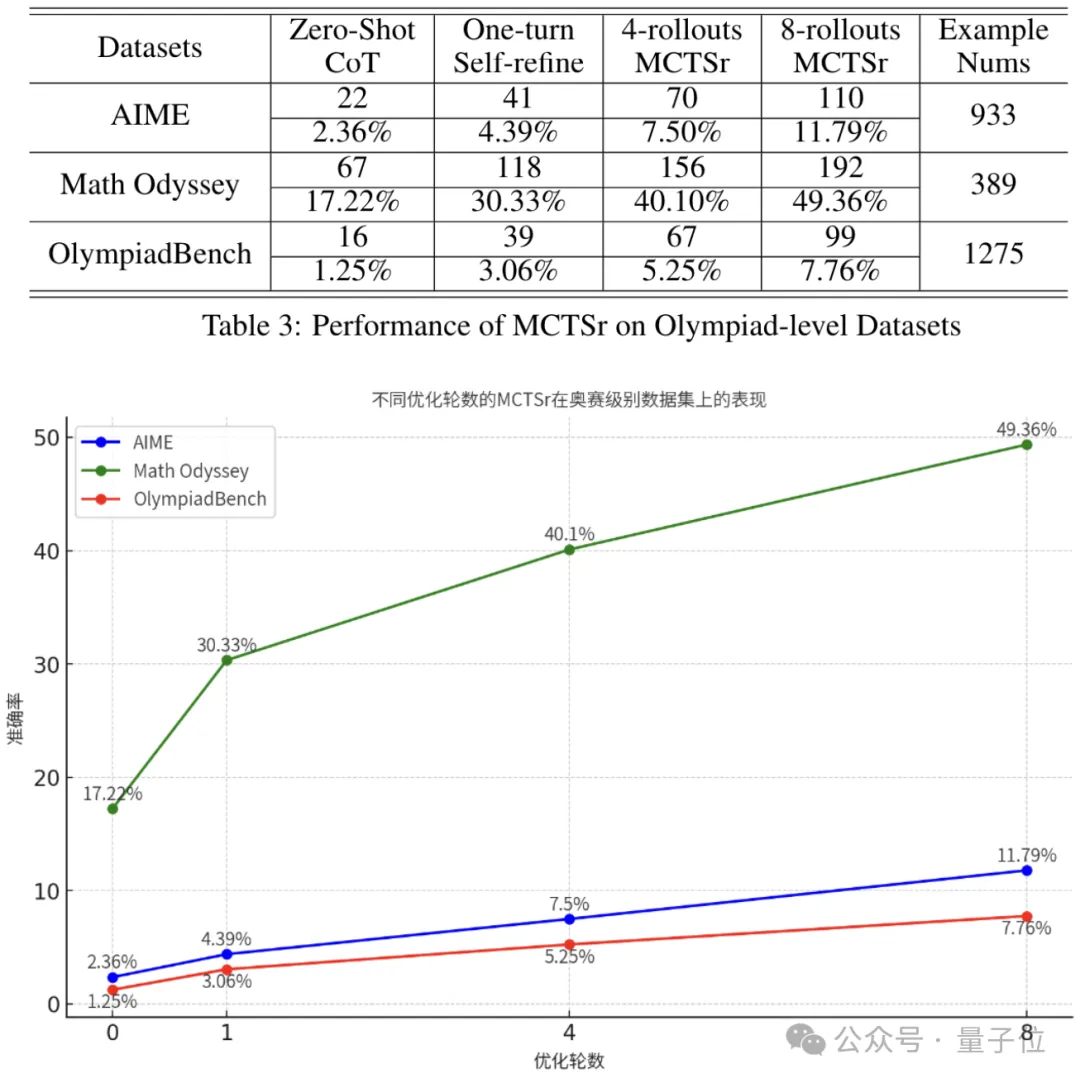
值得一提的是，Math Odyssey数据集在2024年4月才发布，其内容与Llama 3的预训练语料重叠度很低。

而在这个数据集上，MCTSr模型的性能从Zero-Shot CoT的17.22%提升到了8-rollouts MCTSr的49.36%。

这一结果表明，MCTSr在面对全新的问题时，已经显现出了一定的泛化能力。

目前，MCTSr的代码已经开源，感兴趣的读者可以到GitHub当中了解。

论文地址：

https://arxiv.org/abs/2406.07394

GitHub：

https://github.com/trotsky1997/MathBlackBox

文章来源于：微信公众号量子位，作者：克雷西