想参加陶哲轩发起的「众包」数学研究项目吗？

机会来了！

AI辅助证明数学研究，越来越可行了

在传统上，一个数学研究项目通常是由1到5名数学专家来完成的。

他们每个人都对项目的各方面都足够熟悉，可以验证彼此的贡献。

但如果要组织起更大规模的数学研究项目，特别是涉及公众贡献的项目，就麻烦多了。

原因在于，很难验证所有人的贡献。

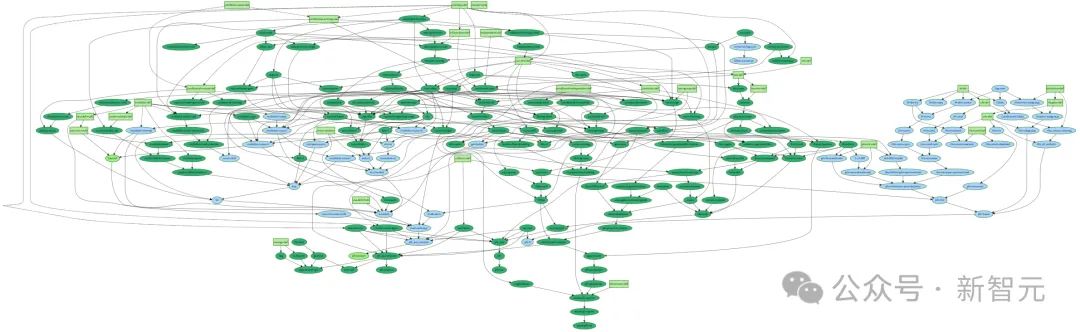
2023年底，陶哲轩宣布：将多项式Freiman-Ruzsa猜想的证明形式化的Lean4项目，在三周后取得了成功（图为最新状态）

要知道，在数学论证某个部分中的单个错误，可能就会使整个项目失败。

而且，以一个典型数学项目的复杂程度来说，期待具有本科数学教育水平的公众做出有意义的贡献，也是不现实的。

由此我们也可以知道，把AI工具纳入到数学研究项目中，也是极有挑战性的。

因为AI会生成看似合理但实际上毫无意义的论证，因此需要额外验证，才能将AI生成的部分添加到项目中。

好在，证明辅助语言（比如Lean）提供了潜在的方法，能够克服这些障碍，并且让专业数学家、广大公众和AI工具的合作成为可能。

这种方法的前提是，项目可以以模块化的方式分解成更小的部分，这些部分可以在不必理解整个项目的情况下就能完成。

目前的例子主要有将现有数学结果形式化的项目（比如对Marton最近证明的PFR猜想的形式化）。

这些形式化工作，主要是通过众包方式由人类贡献者（包括专业数学家和感兴趣的公众）完成的。

同时，还有一些新兴的尝试，试图引入更多的自动化工具来完成，后者包括传统的自动定理证明器，以及更现代的基于AI的工具。

探索全新数学问题，成为可能

并且，陶哲轩还认为，这种全新范式不仅可以用于形式化现有的数学，还可以用来探索全新的数学！

过去，他曾经和继任组织过一个在线协作「Polymath」的项目，就是一个很好的例子。

不过，这个项目没有将证明辅助语言纳入工作流，贡献就必须由人类主持人管理和验证，这项工作非常耗时，也限制了将这些项目进一步扩大。

现在，陶哲轩希望，添加证明辅助语言能突破这个瓶颈。

而他尤其感兴趣的，就是是否可能使用这些现代工具同时探索一类数学问题，而不是一次只关注一两个问题。

本质上，这种方法是可模块化的重复任务，如果有适当的平台来严格协调所有贡献，众包和自动化工具可能会尤其有用。

如果用以前的方法，这种数学问题类型是无法扩大规模的。除非在多年时间里，随着个别论文慢慢地一次探索一个数据点，直到对这类问题获得合理的直觉。

此外，如果有一个大型问题数据集，可能有助于对各种自动化工具进行性能评估，并且比较不同工作流程的效率。

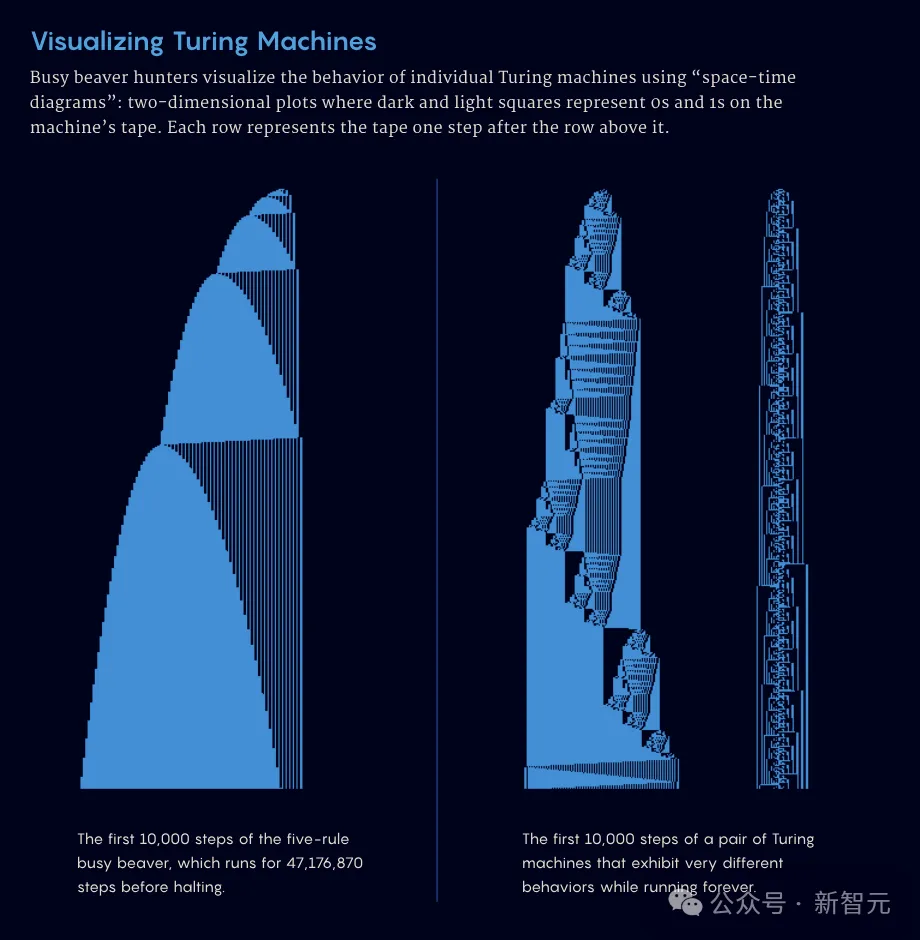
这类项目最近的一个例子，是「忙碌海狸挑战」。

在今年7月，第五个忙碌海狸数被证实为是47,176,870。

一些更早的众包计算项目，比如「互联网梅森素数大搜索」（Great Internet Mersenne Prime Search， GIMPS），在内在精神上跟这些项目也有些类似，尽管它们使用的是更传统的工作量证明机制，而不是证明辅助语言。

陶哲轩表示，很想知道是否还有其他现存的众包项目探索数学空间的例子，以及是否有可用的经验教训。

陶哲轩提出新项目

为此，陶哲轩自己也提出了一个项目，来进一步测试这一范式。

这个项目受到去年MathOverflow问题的启发。

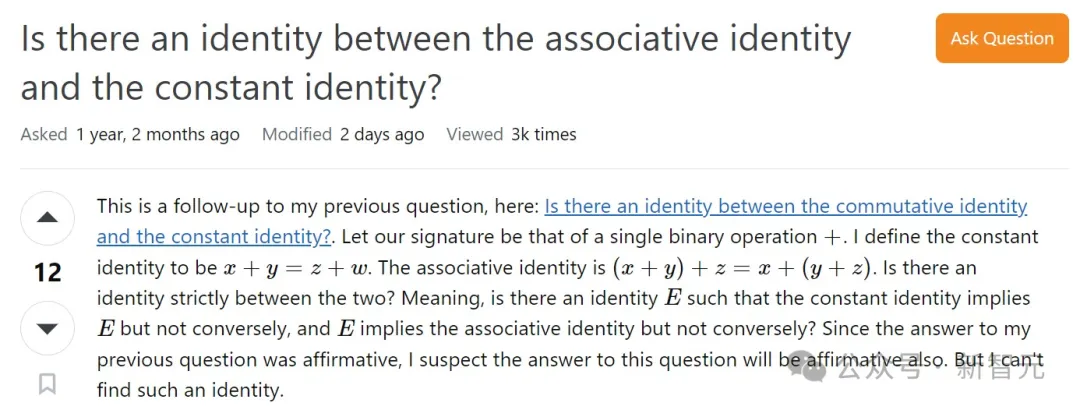
不久后，陶哲轩在自己的Mathstodon上，对它进行了进一步讨论。

这个问题属于泛代数（universal algebra）领域，涉及对原群（magma）的简单等式理论的中等规模探索。

原群是一个配备了二元运算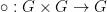的集合G。

最初，这个运算o没有附加任何额外的公理，因此原群本身是较为简单的结构。

当然，通过添加额外的公理，如恒等公理或结合律公理，我们可以得到更熟悉的数学对象，例如群、半群或幺半群。

在这里，我们感兴趣的是（无常数的）等式公理。这些公理涉及由运算o和G中的一个或多个未知变量构建的表达式的相等性。

此类公理的两个熟悉的例子，是交换律x o y = y o x和结合律(x o y) o z = x o (y o z)。

其中x，y，z是原群G中的未知变量。

另一方面，（左）恒等公理e o x = x在这里不被视为等式公理（equational axiom），因为它涉及一个常数e ∈ G。这类涉及常数的公理在本研究中不予讨论。

接下来，为了阐明自己发起的研究项目，陶哲轩介绍了十一个关于原群的等式公理例子。

这些等式公理是仅涉及原群运算和未知变量的等式——

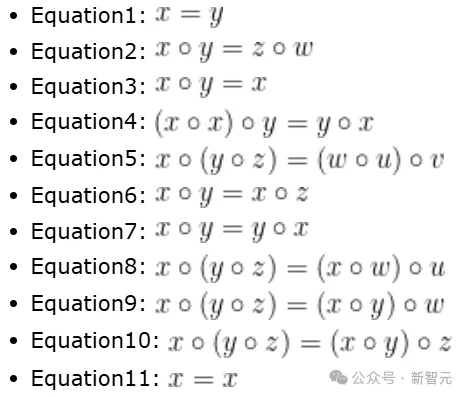
因此，举例来说，等式7表示交换律公理，而等式10表示结合律公理。

常数公理等式1是最强的，因为它限制了原群G最多只能有一个元素；与之相反，自反公理等式11是最弱的，所有原群都满足这一公理。

接下来，我们就可以探讨这些公理之间的推导关系：哪些公理能推出哪些公理？

例如，等式1可以推导出这个列表中的所有其他公理，而这些公理又可以推导出等式11。

等式8作为特殊情况可以推导出等式9，而等式9又作为特殊情况可以推导出等式10。

这些公理之间完整的推导关系可以用以下哈斯图（Hasse diagram）来描述：

这一结果特别回答了数学问答网站MathOverflow上的一个问题：是否存在介于常数公理（等式1）和结合律公理（等式10）之间的等式公理（equational axioms）。

值得注意的是，这里大多数的蕴含关系都很容易证明。然而，其中存在一个非平凡的蕴含关系。

这个关系是在一个与前述问题密切相关的MathOverflow帖子回答中得到的：

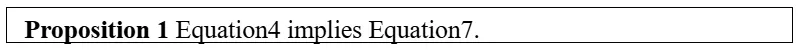
命题1：等式4蕴含等式7

证明：假设G满足等式4，因此

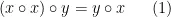
对所有x,y ∈ G成立。

特别是，当y = x o x时，可以得出(x o x) o (x o x) = (x o x) o x。

再次应用（1），可以得出x o x是幂等的：

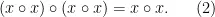
现在，在（1）中将x替换为x o x，然后使用（2），可以得出(x o x) o y = y o (x o x)。

尤其，x o x与y o y是可交换的：

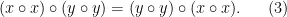
此外，通过两次应用（1），可以得到(x o x) o (y o y) = (y o y) o x = x o y。

因此，（3）就可以简化为x o y = y o x，这就是等式7。

上述论证过程的形式化，可以在Lean中找到。

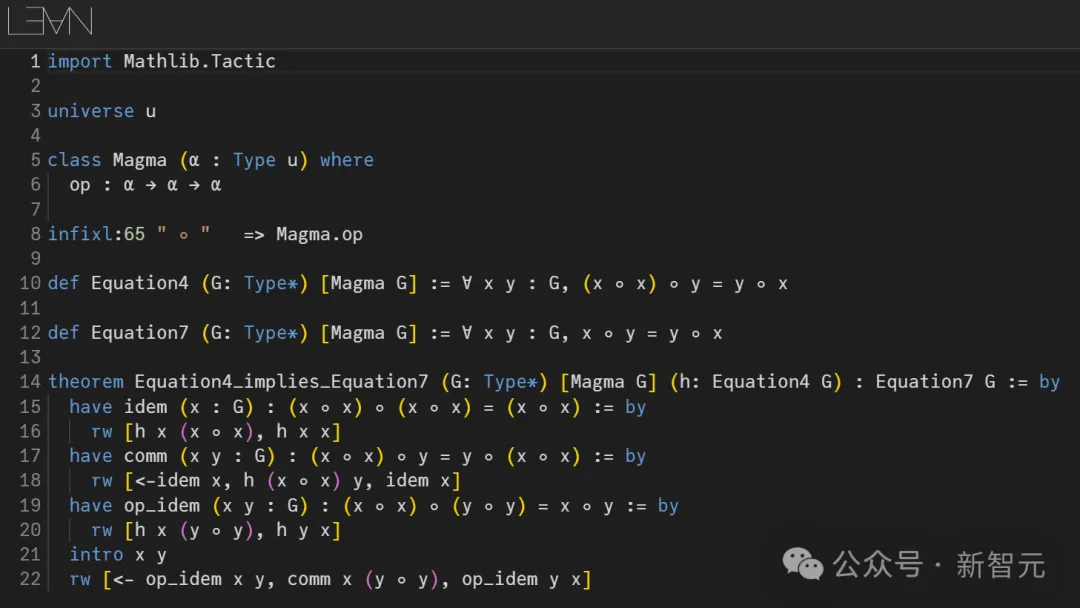
然而值得注意的是，确定一组等式公理是否决定另一组等式公理的一般问题，是不可判定的。

因此，这里的情况有点类似于「忙碌海狸」挑战，即在某个复杂点之后，我们必然会遇到不可判定的问题；但在达到这个阈值之前，我们仍有希望发现有趣的问题和现象。

上面的哈斯图不仅断言了列出的等式公理之间的蕴含关系，还断言了公理之间的非蕴含关系。

例如，如图所示，交换公理等式7并不蕴含等式4公理(x + x) + y = y + x。

要证明这一点，只需找出一个满足交换公理等式7但不满足等式4公理的原群的例子。

比如，在这种情况下，我们可以选择自然数集N，其运算为x o y := x+y。

更一般地，该图断言以下非蕴含关系，这些关系（连同已指出的蕴含关系）完整描述了这十一个公理之间蕴含关系的偏序集：

在此，陶哲轩邀请读者提出反例，来完成其中的部分证明。

最难找到的反例，就是等式9无法推出等式8了。

用Lean可以给出解决方案。

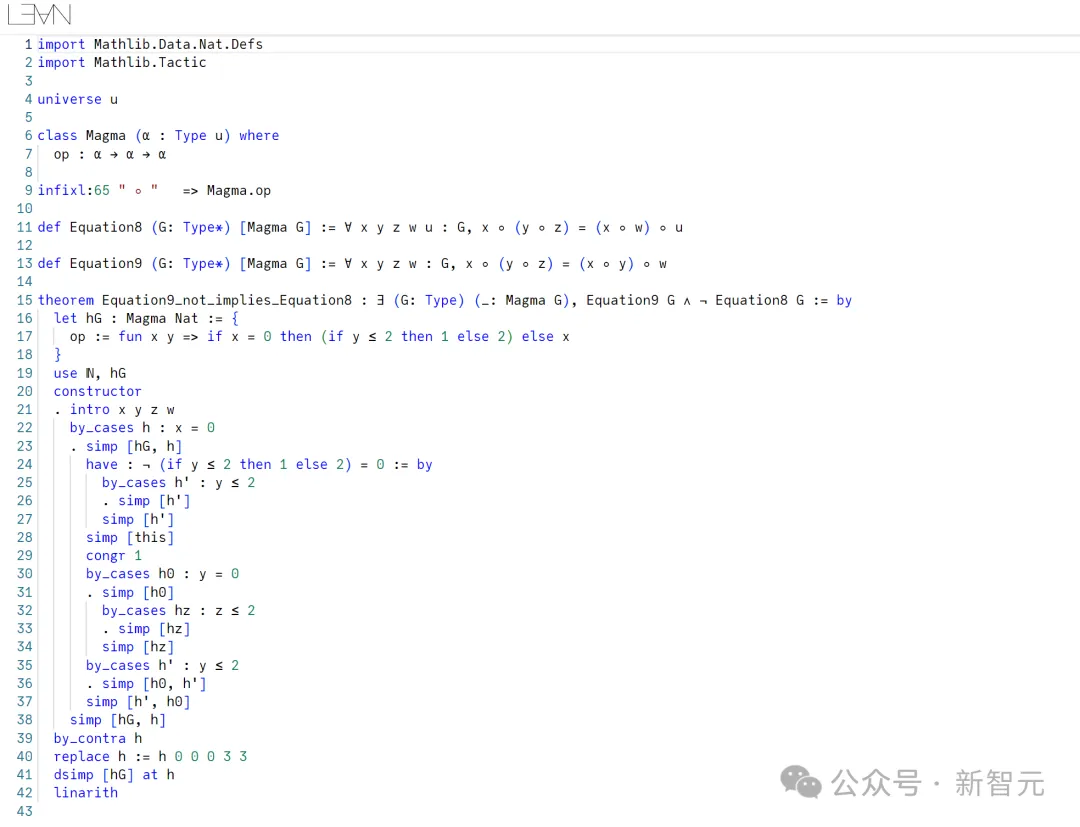
另外，陶哲轩还提供了一个GitHub存储库，包含了所有上述包含和反包含关系的Lean证明。

可以看出，仅仅计算11个等式的哈斯图就已经有些繁琐了。

而陶哲轩提出的项目，是尝试将这个哈斯图扩展几个数量级，覆盖更大范围的等式集。

他提议的集合是ε，即最多使用原群运算o四次的等式集，直到重新标记和等式的自反性和对称性公理。

这包括了上述十一个等式，但还有更多。

还有多少呢？

回想一下，卡特兰数C_n是用二元运算o（应用于n+1个占位符变量）形成表达式的方法数；而给定m个占位符变量的字符串，贝尔数B_m是为这些变量分配名称的方法数（可以重新标记），其中允许某些占位符被分配相同的名称。

因此，忽略对称性，最多涉及四次运算的等式数量是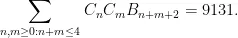

左侧和右侧相同的等式数量是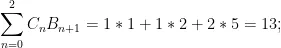

这些都等同于自反公理（等式11）。

剩下的9118个等式由于等式的对称性成对出现，所以ε的总大小是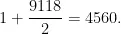

陶哲轩表示，自己还没有生成这样恒等式的完整列表，但他猜想，使用Python就可以轻松完成。

使用AI工具，应该能生成大部分所需的代码。

他表示，自己完全不清楚ε的几何结构会是什么样子。

大多数等式会彼此不可比较吗？它会分为「强」公理和「弱」公理吗？

现在，陶哲轩的留言区，已经有了几十条评论。

感兴趣的读者，陶哲轩也向你发出了邀请。

参考资料：

https://terrytao.wordpress.com/2024/09/25/a-pilot-project-in-universal-algebra-to-explore-new-ways-to-collaborate-and-use-machine-assistance/

文章来自于微信公众号“新智元”