多视图自监督学习（MVSSL，或称为联合嵌入自监督学习）是一种强大的无监督学习方法。它首先创建无监督数据的多个转换或视图，然后以类似监督的方式使用这些视图来学习有用的表示。

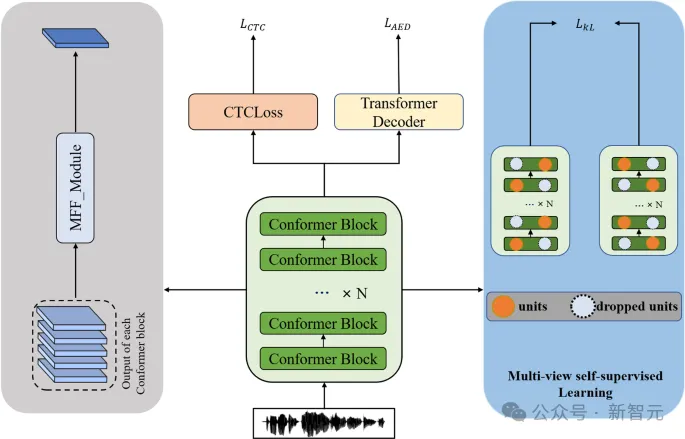
实现MVSSL的具体方法有很多，但大致可以分为四类：对比、聚类、蒸馏/动量、冗余减少。

在这众多的方法中，最大流形容量表示（Maximum Manifold Capacity Representation，MMCR）是与众不同的一类。

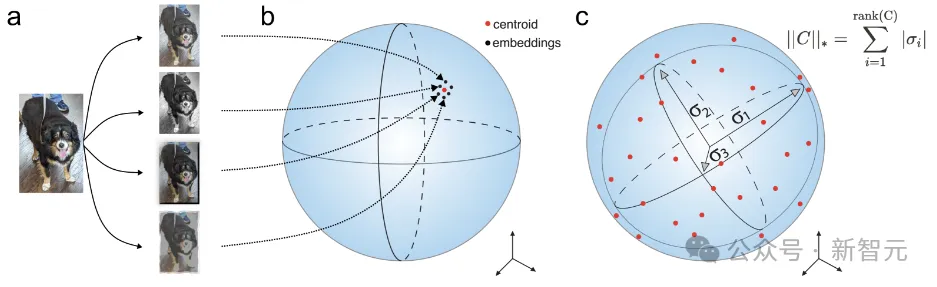
MMCR不明确使用对比，不执行聚类，不利用蒸馏，也不明确减少冗余，但效果却可以媲美甚至超越其他领先的MVSSL方法。

而来自斯坦福、MIT、纽约大学和Meta-FAIR等机构的研究人员，正在通过新的研究重新定义这个框架的可能性。

论文地址：https://arxiv.org/pdf/2406.09366

作为论文作者之一，LeCun也发推表达了自己的观点：

除非使用预防机制，否则使用SSL训练联合嵌入架构会导致崩溃：系统学习到的表示信息不够丰富，甚至是恒定不变的。

人们设计了多种方法来防止这种崩溃。

一类方法是样本对比：确保不同的输入产生不同的表示。

另一类是维度对比：确保表示的不同变量对输入的不同方面进行编码。

两种类型的方法都可以从信息最大化参数中派生出来：确保表示形式尽可能多的编码有关输入的信息。

方差-协方差正则化、MMCR和MCR2（来自伯克利大学马毅团队）都是infomax维度对比方法。

信息最大化维度对比方法的核心思想，是推动编码器学习输入的表示，使其尽可能充分地利用表示空间，就像在有限的画布上尽可能展现丰富的细节。

为了更好地理解MMCR，研究人员利用高维概率工具证明了，MMCR可以激励学习嵌入的对齐和均匀性。

同时，这种嵌入最大化了视图之间的互信息的下界，从而将MMCR的几何视角与MVSSL中的信息论视角联系起来。

为了更好地利用MMCR，研究人员对预训练损失的非单调变化进行数学预测和实验确认，发现了类似于双下降的行为。

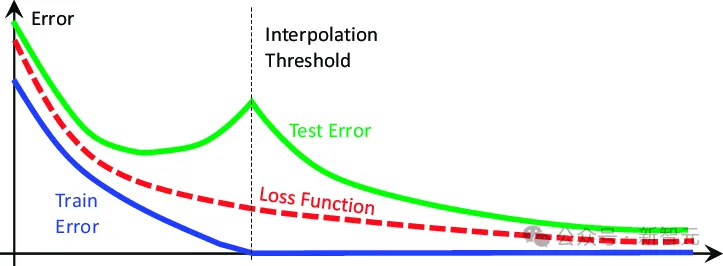
此外，研究人员还发现了计算上的scaling law，可以将预训练损失预测为梯度步长、批量大小、嵌入维度和视图数量的函数。

最终，作者证明了这个最初应用于图像数据的MMCR方法，在多模态图像文本数据上同样表现优异。

MMCR

MMCR由纽约大学数据科学中心（NYU Center for Data Science，CDS）的研究人员于2023年提出。

该方法源于神经科学中的有效编码假说：生物感觉系统通过使感觉表征适应输入信号的统计数据来优化，例如减少冗余或维度。

最初的MMCR框架通过调整「流形容量」（衡量给定表示空间内可以线性分离的对象类别数量的指标）将这一想法从神经科学扩展到了人工神经网络。

许多MVSSL方法要么明确源自信息论，要么可以从信息论的角度来理解，但MMCR不同。

MMCR指出估计高维互信息已被证明是困难的，且逼近互信息可能不会改善表示。MMCR的基础在于数据流形线性可分性的统计力学表征。

不过LeCun等人的这篇工作，将MMCR的几何基础与信息论原理联系起来，探索了MMCR的更深层次机制，并将其应用扩展到了多模态数据，例如图像文本对。

理论基础

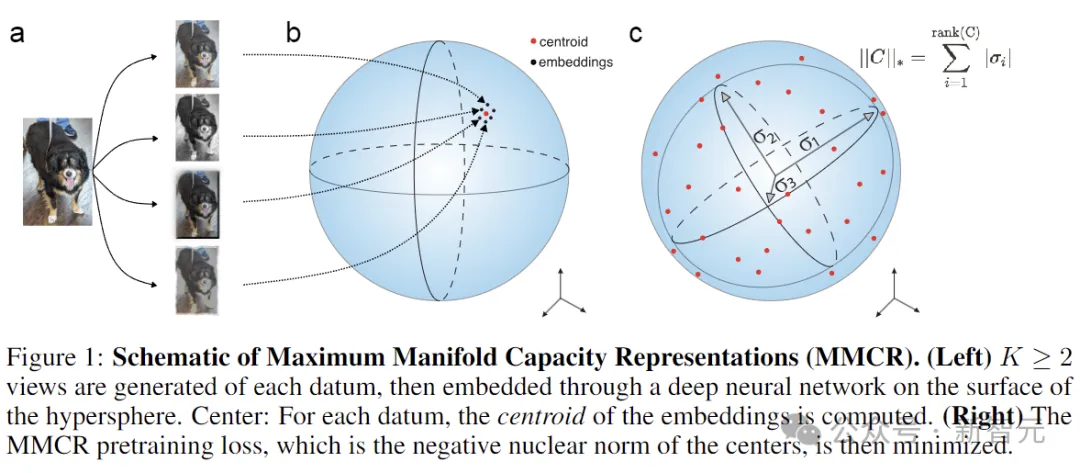
MMCR源自有关线性二元分类器性能的经典结果。考虑D维度中的P点（数据），具有任意分配的二进制类标签；线性二元分类器能够成功对点进行分类的概率是多少？

统计力学计算表明，在热力学极限下，容量α= 2时会发生相变。MMCR将此结果从点扩展到流形：

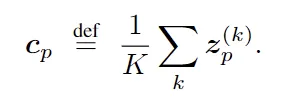
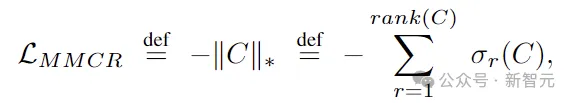
最小化MMCR损失意味着最大化平均矩阵的核范数。

直观上，完美重建意味着同一数据的所有视图都被网络映射到相同的嵌入，完美均匀性意味着嵌入均匀分布在超球面周围。

具有完美重建和完美均匀性的嵌入实现了尽可能低的MMCR损失

基于对MMCR嵌入分布的新认识，我们如何将MMCR的统计力学几何观点与信息论观点联系起来？

答案是，MMCR激励表示的最大化，对应于同一数据的两个视图的两个嵌入共享的互信息的下限。

考虑某些输入数据两个不同视图的嵌入之间的互信息。两个视图之间的互信息必须至少与两项之和一样大：一个嵌入重建另一个的能力，再加上嵌入的熵：

MMCR的双下降

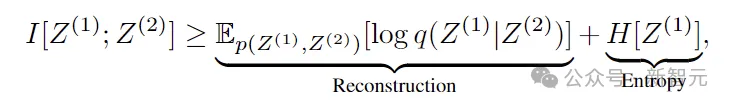
通过高维概率分析可知，预测最大流形容量表示的预训练损失，也应该在其预训练损失中表现出非单调双下降样行为。

（双下降：测试损失作为数据总数和模型参数数量的函数表现出非单调变化 ）。

然而，本文的分析也表明，这种类似双下降的行为应该发生在非典型参数（流形的数量P和维数D）上，而不是数据的数量和模型的参数量。

具体来说，理论预测最高的预训练误差应该恰好发生在阈值P = D处，预训练误差落在阈值的两侧。

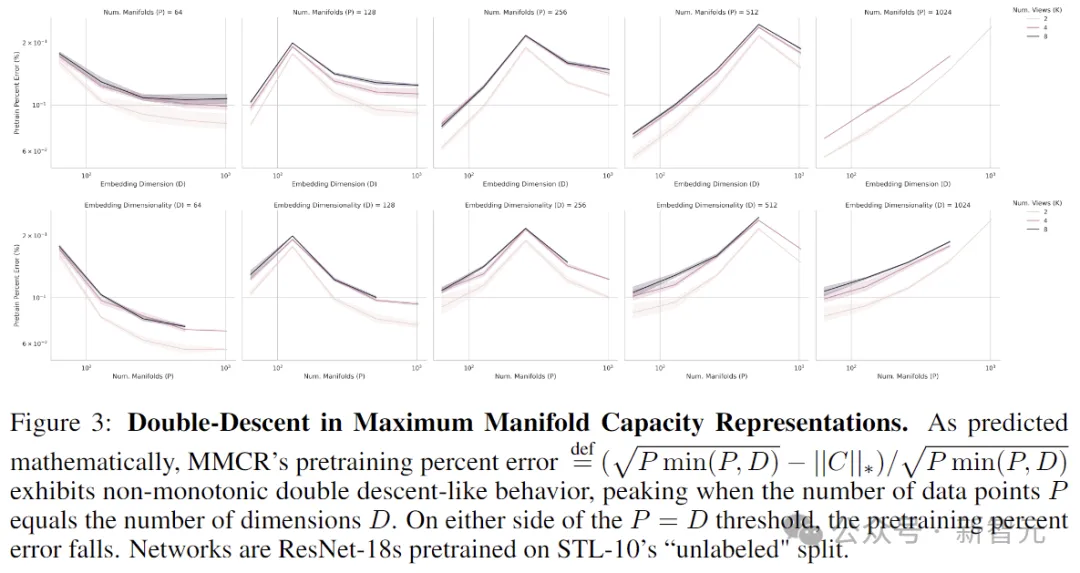
为了比较不同超参数对的点数P和数据维度D之间的损失，这里使用MMCR预训练界限来定义预训练百分比误差：

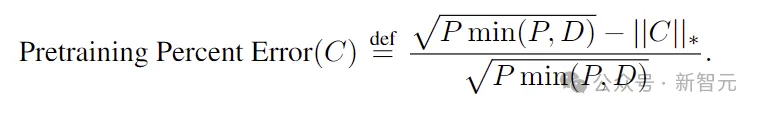
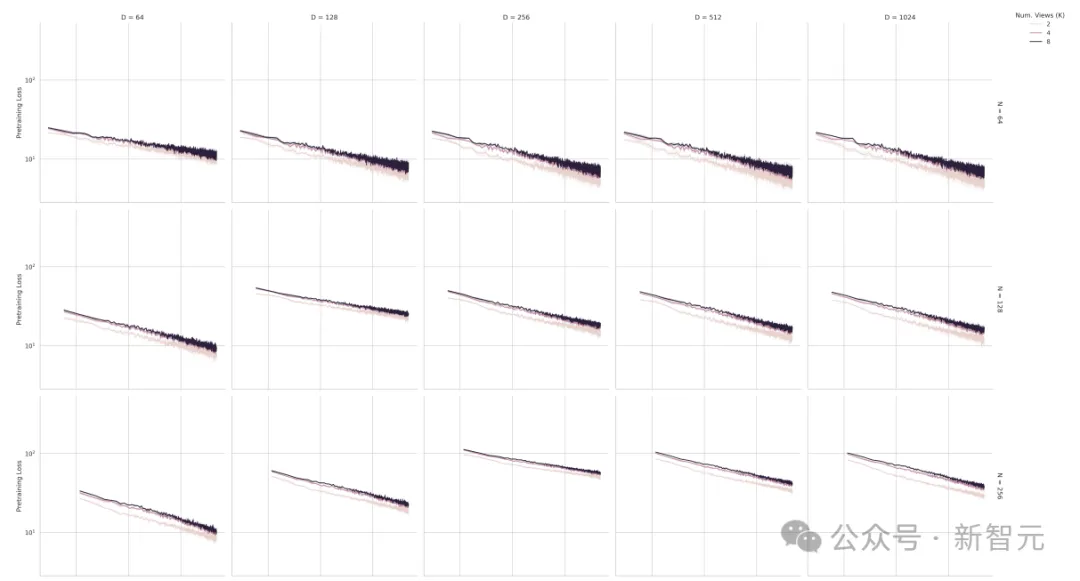
研究人员在STL-10上预训练了ResNet-18，STL-10是一个与CIFAR-10类似的数据集，但分辨率更高 (96x96x3)，并且包含100000张图像的附加未标记分割。

扫描范围P：{64, 128, 256, 512, 1024} × D：{64, 128, 256, 512, 1024} × K：{2, 4, 8}（K为视图数），结果如上图所示。

Compute Scaling Laws

在许多MVSSL方法中，更改超参数通常会导致预训练损失不相称，从而使运行之间的比较变得困难。

然而，MMCR预训练百分比误差产生的数量介于0和1之间，因此可以将不同超参数（P和D）时的训练情况放在一起比较。

执行这样的比较会产生有趣的经验现象：计算MMCR预训练百分比误差中的神经缩放定律。

通过绘制在STL-10上预训练的ResNet-18网络，我们可以清楚地看到预训练百分比误差的幂律缩放与所有点数P 、嵌入维度D和视图数量K的计算量的关系。

一个关键细节是这些神经缩放曲线突出了类似双下降的行为：对角线子图（P = D时）具有较高的预训练百分比误差和较小的预训练百分比斜率。

MMCR与多模态

考虑OpenAI的对比语言图像预训练模型CLIP的设置，两个不同的网络在图像文本标题对上进行预训练，从两个不同的数据域X和Y获取数据。

X和Y是配对的，使得X中的每个示例在Y中都有对应的正对，反之亦然。从MMCR角度来看，X和Y可以理解为同一底层对象的两个视图。

因此，最优变换嵌入f(X)和g(Y)应映射到同一空间，并且我们可以利用对MMCR的改进理解来训练这些最优网络。

与常见的MVSSL不同，这里的X和Y在实践中可能代表极其不同的分布。

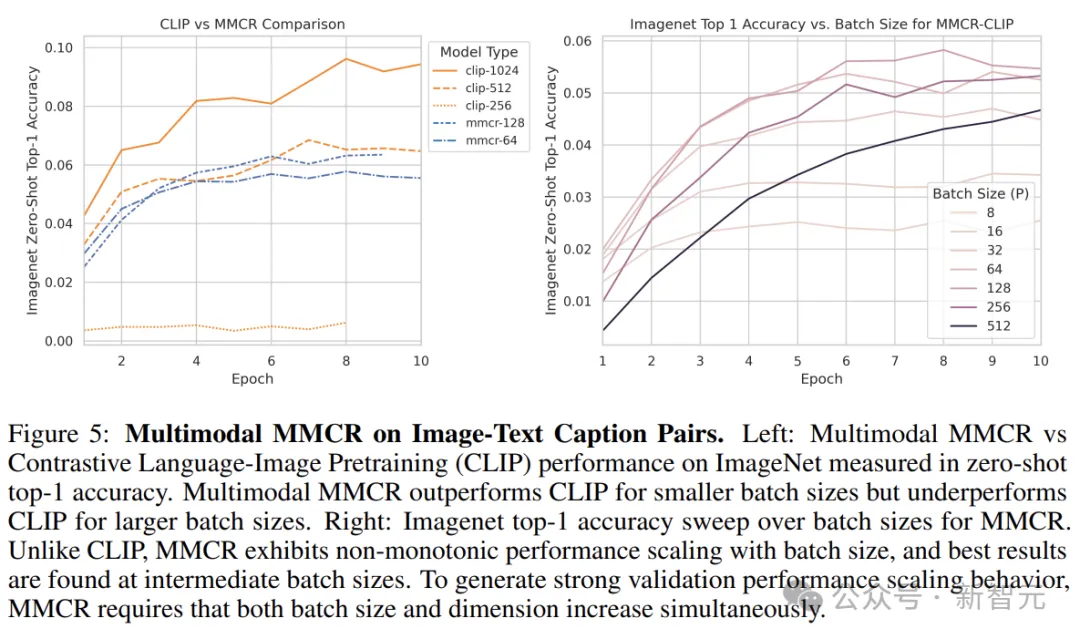
在上图的图像-文本对齐实验中，作者将多模态MMCR应用于DataComp-Small，并将零样本Imagenet性能与标准CLIP目标进行比较。

可以发现，多模态MMCR在小批量（< 512）下表现优于CLIP。

参考资料：

https://x.com/ylecun/status/1834666512856031537

文章来自于微信公众号“ 新智元”