黎曼猜想，竟被Grok 3「证明」了？

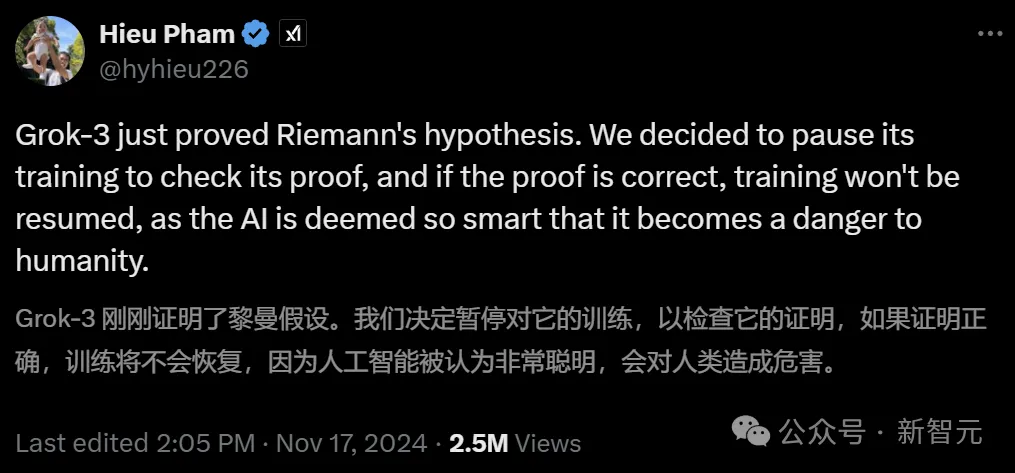
为此，xAI暂停了Grok 3的训练来验证它的证明，如果结果是正确的，将会完全终止模型的训练。

xAI工程师Hieu Pham在社交媒体的最新「爆料」，成为AI圈最火爆的话题。

要知道，黎曼猜想是千禧年七大数学难题之一，被誉为「猜想界的皇冠」。

2000年，黎曼猜想被美国克雷数学研究所（Clay Mathematics Institute of Cambridge，CMI）指定为「七大千禧年难题之一」

由于信息量太大，网友们直接被整懵了，分不清这是真的还是在玩梗……

几个小时之后，在Pham另一个帖子中，证明了这只是自己的调侃。

恶搞的起因是，一位网友Andrew Curran最先「爆料」，传言称Grok3在训练时发生了灾难性事件。

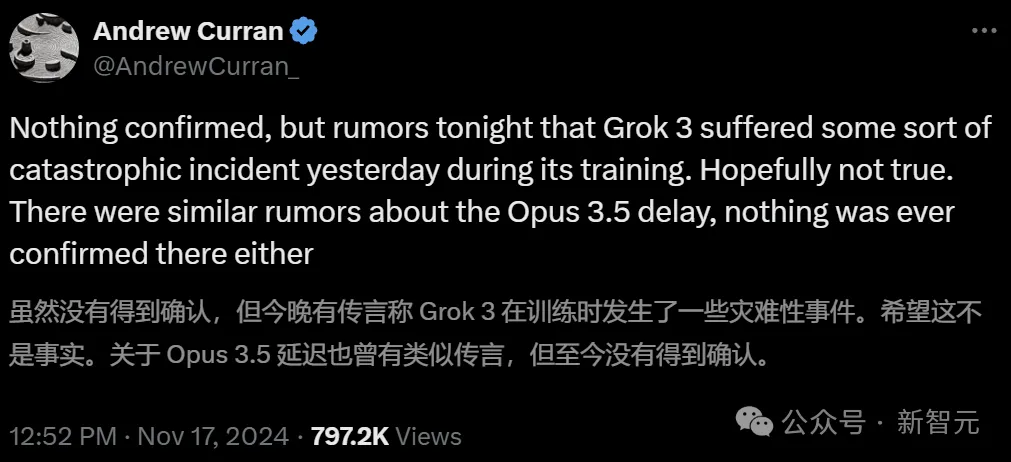
明眼的网友很快便质疑道：LLM训练怎么会出现灾难性事件？

即便是出现loss激增，也只需要回到上一个Checkpoint，调整一下，就可以接着训了。

除非是服务器全烧了，数据全都不剩了……

眼瞧着消息越传越广，xAI联创Greg Yang坐不住了。

对此，他用讽刺的语气调侃道：「对对对，Grok 3训着训着突然开始攻击办公室的保安了。」

另一位研究人员Heinrich Kuttler也接梗道：「对对对，情况非常糟糕！我们后来用nan（Not a Number，非数）把所有坏的权重都替换了一遍，才恢复。」

网友见状，也跟着玩起了梗。

要攻克黎曼猜想，还差些什么？

言归正传，让我们来仔细看一下，目前人类离攻克黎曼猜想还差几步。

如今，「黎曼猜想」就像是一座巍峨的高峰，165年来从未有人成功攀上。

它就像大海中的灯塔，为数学领域的发展指明方向：很多数论和复变函数领域的工作都基于黎曼猜想为真这个前提，因此一旦证明了黎曼猜想，许多其他工作也会得到完整的证明。

黎曼猜想起源于德国数学家高斯，他给出了一个公式，能够近似地预测出任意数字的素数个数。

在1859年，德国数学家波恩哈德·黎曼改进了高斯的公式，用涉及复变量函数演算的方法，得出一个原创公式。

这就是赫赫有名的「黎曼猜想」。

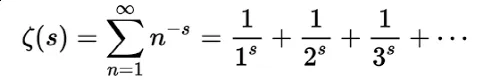
根据公式，能够画出无穷多个点。黎曼猜测，这些点有一定的排列规律，一部分在一条横线上，另一部分则在一条竖线上，所有点都在两条直线上排列，无一例外。

黎曼ζ函数可视化

理论上，无法证明是否所有的点都在这两条线上，但是，只要有一个点不在，就能推翻黎曼猜想！

现在，数学家们已经用计算机验证了最初的15亿个点，全部符合黎曼猜想。

2022年，张益唐发表111页论文，宣布本质上已证明朗道-西格尔零点问题——广义黎曼猜想的一种特殊且弱得多的形式。

虽然是一个弱一点的形式，但本质上已经是解决了朗道—西格尔零点问题。

用他的话说就是，关于零点猜想问题，「大海里的针我没捞到, 但海底地貌我探得差不多了」。

论文链接：https://arxiv.org/abs/2211.02515

2024年，陶哲轩力推MIT数学教授Larry Guth和牛津大学菲尔兹奖得主James Maynard的一篇新论文，认为两人在证明黎曼猜想方面取得了重大突破。

过程中，他们牺牲了一枚弃子，情况虽然变得更棘手，却反而离答案更近了。

论文地址：https://arxiv.org/abs/2405.20552

当然，尽管我们离完全解决这一猜想还很遥远。

AI的数学能力，到底什么水平？

这么说起来，目前的AI是否真的有证明黎曼猜想的能力呢？

我们可以来看看，爆火全网的AI证明工具AlphaProof，是如何做出IMO 2024的三道题的。

从某种角度来说，IMO数学竞赛题跟「猜想界的皇冠」黎曼猜想距离有多远，那离AI证明黎曼猜想也就有多远。

谷歌DeepMind研究人员，AlphaProof负责人Rishi Mehta最新博客中，介绍了AlphaProof在IMO中的最新表现。

4个月前，谷歌DeepMind团队发布了两个数学推理新模型AlphaProof和AlphaGeometry 2。

前者在破解IMO 2024六道竞赛试题中，做对了其中4道，而且每道题拿下了满分，相当于银牌选手水平（28分）。

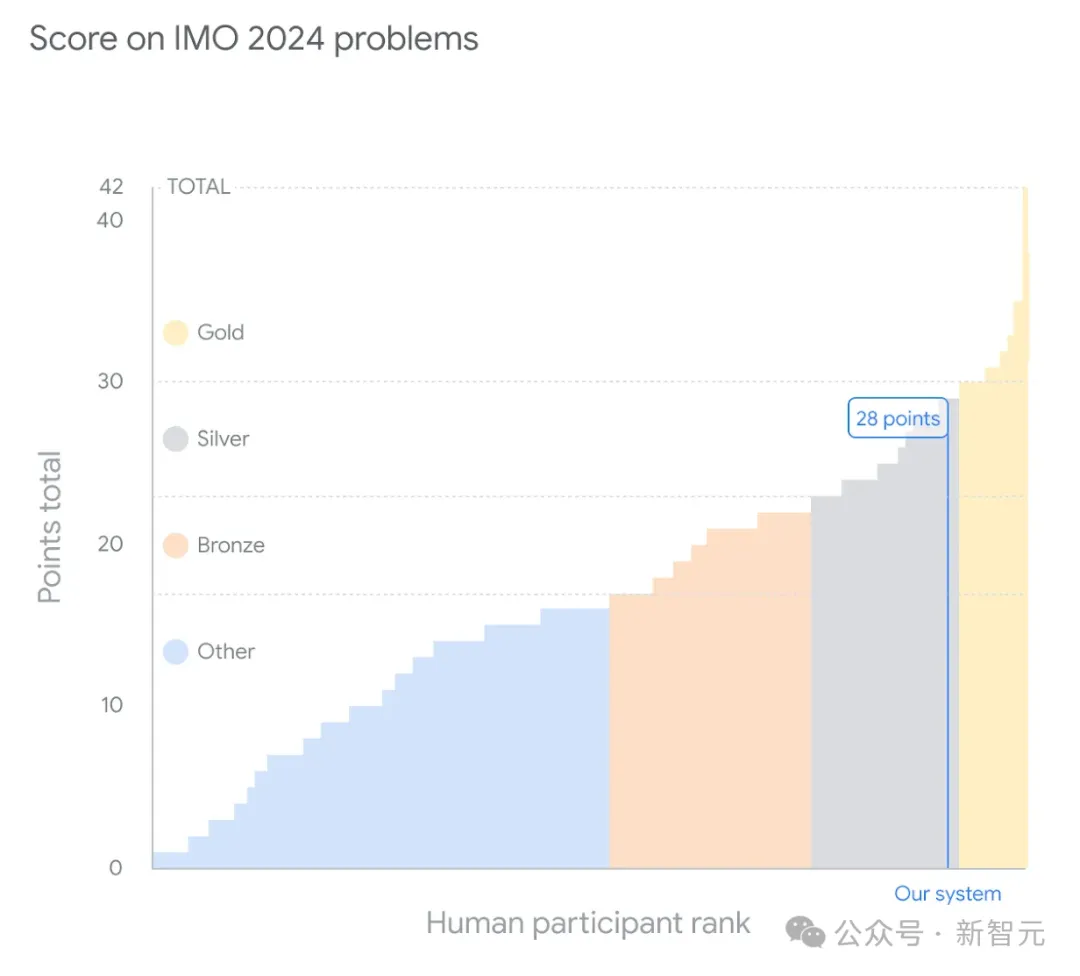
而在最新进展文章中，Mehta揭示了AlphaProof在IMO 2024解题中最酷的想法。

在证明过程中，AlphaProof会使用到Lean 生成证明，并且每个Lean证明由一系列策略组成。

因此，Mehta将挑选出对应于这些想法的策略，针对AlphaProof解决的第 1、2和6题进行分析。

问题 1

问题

确定所有实数α，使得对于每一个正整数n，整数⌊α⌋+⌊2α⌋+⋯+⌊nα⌋是n的倍数。（注意，⌊z⌋表示小于或等于z的最大整数。例如，⌊−π⌋=−4 和⌊2⌋=⌊2.9⌋=2。）

解答

答案是所有偶整数。

需要注意的是，AlphaProof解决这些问题的方式是，提出许多解答候选者，尝试证明和反驳每一个，最终仅为正确答案找到证明。

这里看到的证明是，证明答案是偶整数集的那个。

证明偶整数满足给定性质显而易见，而这个证明的难点在于，证明除了偶整数之外没有其他α能够满足它。

AlphaProof以一种有趣（尽管复杂）的方式做到这一点：

它首先设定一个整数ℓ，使得 2ℓ=⌊α⌋+⌊2α⌋。这是成立的，因为通过将n=2代入给定性质，便可知道右侧是偶数。

existsλx L=>(L 2 two_pos).rec λl Y=>?_

L 2是在n=2的情况下使用给定性质。此外，AlphaProof经常将几个策略组合在一行中。一个更易理解的版本是：

constructor· intro x Lobtain ⟨l, Y⟩ := L 2 (by exact two_pos)

注意，我们还将α重命名为x。接下来，它声称（并继续证明）对于所有自然数 n，⌊(n+1)α⌋=⌊α⌋+2n(ℓ−⌊α⌋) ……（1）.

suffices: ∀ (n : ℕ),⌊(n+1)*x⌋ =⌊ x⌋+2 * ↑ (n : ℕ) * (l-(⌊(x)⌋))

从中，它能够得到α=2(ℓ−⌊α⌋)。

use(l-⌊x⌋)*2

这必须是一个偶整数（因为它是一个整数乘以 2）。

它证明这些事情的方式涉及一些相当复杂的简化。但设置（1）中的声明是使其余证明成立的令人印象深刻的一步。

Mehta称，对我来说，这一声明的动机相当不直观，而事实上一切都能奏效几乎是神奇的。

AlphaProof的完整解决方案如下：

上下滑动查看

问题 2

问题

找到所有满足条件的正整数对(a,b)，使得存在正整数g和N，使得gcd(an+b,bn+a)=g对于所有整数n≥N成立。

解答

AlphaProof正确给出 (1,1) 是唯一的解。

为了证明没有其他解可以成立，它要求我们考虑数ab+1。它声称（并随后证明）ab+1必须整除g。

suffices:b.1*b.2+1∣Y

需要注意的是，AlphaProof决定将对 (a,b) 重命名为b，以便它必须将元素引用为b.1和b.2。出于某种原因，它还选择将变量g重命名为 Y。

现在，选择n=Nϕ(ab+1)，可以得到(ab+1)∣(aNϕ(ab+1)+b) 和 (ab+1)∣(bNϕ(ab+1)+a)。

由于ab+1与a和b互质，因此可以应用欧拉定理，即

aϕ(ab+1)≡1(modab+1)

bϕ(ab+1)≡1(modab+1)

所以有ab+1∣1+b和ab+1∣1+a，由此可以得出a=b=1。

这一策略紧密地遵循了人类对此问题的证明。选择考虑ab+1是构建证明的巧妙想法。

AlphaProof 的完整解决方案如下：

问题 6

问题

设Q是所有有理数的集合。一个函数f:Q→Q被称为aquaesulian函数，如果对于每个x,y∈Q，满足以下性质：f(x+f(y))=f(x)+y或f(f(x)+y)=x+f(y)。

证明存在一个整数c，使得对于任何aquaesulian函数f，形式为f(r)+f(−r)的有理数最多有c个不同的值，并找出c的最小可能值。

解答

AlphaProof求解答案为c=2，证明过程分为两部分。

首先，它通过证明f(r)+f(−r)只能是0或某个单一的其他值来证明c≤2。这部分证明相当复杂，并巧妙地利用了给定的aquaesulian性质。

完成这一步后，c可以是1或2。

为了证明 c=2，AlphaProof提出了一个aquaesulian函数 f(x)=−x+2⌈x⌉，使得 f(r)+f(−r)取两个不同的值。

specialize V $ λ N=>-N+2 *Int.ceil N

然后它展示了f(−1)+f(1)=0和f(1/2)+f(−1/2)=2，这给出了需要的两个不同的值。

use Finset.one_lt_card.2$ by exists@0,V.1.mem_toFinset.2 (by exists-1),2,V.1.mem_toFinset.2 (by exists 1/2)

再次，很多内容被压缩到一行中，但通过exists -1和 exists 1/2展示了两个不同的值。

这是一个值得注意的函数构造，而且相当难以找到！在509名参与者中只有5人解决了 P6，值得注意的是Tim Gowers在评审这个解决方案时也尝试了一下，但没有找到一个能给出两个不同值的函数。

毕竟，IMO 2024第六题被称为「终极boss」，可不是那么轻易就解决掉的。

AlphaProof的完整解决方案如下：

AI距离千禧年难题，还有多远？

关于AI究竟能做什么程度的数学题，网友们也就此展开了讨论。

很多人认为，数学将是AI最先突破的领域之一，因为存在一个可用的既便宜又快速的反馈循环。

数学具有这样的特性：你可以以很少的成本，100%去验证你所做的事是否正确。

而相对于Lean之类的数学证明工具来说，AI验证实验的成本（时间、精力、金钱、安全）都要高出许多数量级。

有网友脑洞大开预测道：数学前沿运动的加速，值得人类建更多发电站！

不过，有一名数学家却在评论区现身说法，认为并不值得用AI这么做。

在他看来，计算时间/成本与问题复杂性之间的权衡，值得严肃考虑。

理论上讲，用形式语言找到证明是一件很轻松的事，因为只需一直搜索可能的证明，直到找到所需陈述结尾的证明就可以了。

计算的并行化程度如何，硬件能力有多大，AI工具对于数学问题的优化程度如何，都会决定AI用多长时间把证明做出来。

但要说专门建数据中心和发电站，把大量能源用于做数学题，他觉得没有必要——因为这并不是为了数学界的利益，而是硅谷大厂们自己的愿景。

不过如果进一步设想，现在的Alphaproof如果变成具有天文数字计算资源的定理证明器，我们或许有一天就可以证明「P/NP问题」。

因为，任何可证明的定理，都可以通过耐心地使用穷举法，列举所有可能的证明来找到。

如果存在一个有限的、格式良好的公式，该公式具有该定理作为结果，那么该定理就可以根据定义证明。

而如果说LLM有什么用处，那就是寻找出令人惊讶的联系，以人类搜索之外的方式，应用现有工具。

AI通过帮助人类解决引理、检查错误、形式化证明，来加速数学研究，在肉眼可见的未来几年内，即将成为现实。

而在去年，微软亚洲研究院、北大、北航等机构的研究人员，就已经通过97个回合的「苏格拉底式」严格推理，成功让GPT-4得出了「P≠NP」的结论。

而这97轮对话，可以说构建出了一个极难的NP完全问题，其中一些实例在时间复杂度低于O(2^n)（即穷举搜索）的情况下是不可解的，也就是说，证明结论为P≠NP。

论文地址：https://arxiv.org/abs/2309.05689

当然，这个证明过程并不严谨，作者用一个假设（假定任意CSP问题的精确算法都有一个等价的分治算法），绕过了P≠NP问题的难点。

其实，像Christian Szegedy这样的AI专家已经做过此类预测：到2026年底，AI将成为「超人数学家」，解决出黎曼猜想等问题。

离AI解决P/NP问题、黎曼猜想这样的的千禧年难题，还会有多远呢？

马斯克曾许诺，用10万块H100训练的Grok 3将在年底发布，应该会令人惊叹。

而如今，这个规模已经扩展到了20万台，再给一点时间，说不定Grok 3真能出奇迹。

参考资料：

https://x.com/TheGregYang/status/1858027187296936428

https://x.com/hyhieu226/status/1858028679747829769

https://rishimehta.xyz/2024/11/17/alphaproofs-greatest-hits.html

文章来自于微信公众号“新智元”