联通破解扩散模型速度质量零和博弈，推理速度提升5倍丨CVPR 2025 Highlight

从“在线训练”到“离线建图”，扩散模型速度再突破！

2025年初，一篇名为ShortDF的论文悄然登上CVPR 2025 Highlight，但在当时并未引起太多圈外关注。

然而半年后，当NeurIPS 2025 Spotlight论文LeMiCa横空出世，人们才意识到：原来两篇文章系出同源。

△ShortDF论文

均由中国联通数据科学与人工智能研究院核心团队参与，并集中在图论结合扩散模型方向上：

如果说ShortDF是该路径的理论先行者，它基于在线训练模式，验证了图论加速的极致潜力；

那么LeMiCa则进一步拓展了这一理论的边界，它创造性地构建了离线建图新范式，成功将图论思想适配到了更高维度的文生图/视频生成任务中。

△ShortDF路径优化策略

所以要想真正理解这条技术演进脉络，有必要追根溯源，重读这篇为后续研究提供了思想火花的ShortDF。

下面是更多详细内容。

核心痛点：迷失在“弯曲”的去噪路径中

在文生视频（如Sora）与文生图（Stable Diffusion）爆发的当下，昂贵的推理开销仍是阻碍实时应用的最大路障。

而扩散模型之所以进展缓慢，本质上是因为其去噪轨迹是一条高度非线性的弯曲路径。

为了逼近这条弯曲路径，现有方案往往面临“零和博弈”：

• 数值求解器（Numerical Solvers）：
• 如DDIM、DPM-Solver。它们试图用较少的步数拟合曲线，但在极低步数（<5步）下，线性近似带来的截断误差会导致画质崩塌，细节严重丢失。

• 蒸馏方法（Distillation）：
• 虽然能强制“一步到位”，但往往需要昂贵的重训练成本，且难以在复杂的高维分布中保持原模型的生成多样性。

那么既然路径弯曲是核心症结，那为何不直接寻找两点间的“直线”？

ShortDF的突破之处，正是在于它引入了“最短路径优化”的思路，试图在训练阶段直接拉直这条轨迹，从而打破速度与质量的制约。

核心机制：ShortDF 的“三板斧”

ShortDF的核心洞察在于：去噪过程本质上是对初始误差（即第一次去噪估计误差）的修正过程。

研究团队打破常规，从误差传播的本质出发，构建了以下“三板斧”策略：

1、锁定“误差上界”，从源头优化。

ShortDF作者深入分析发现，去噪路径的选择空间极其庞大，误差传播难以捉摸，然而初始误差（Initial Residual）实际上构成了当前时刻去噪误差的“上界”。

所以初始误差越小，意味着去噪过程的误差上界就越低。

ShortDF创新性地将优化目标聚焦于初始残差，即当前时刻对的估计误差。

只要压低了这个“天花板”，后续去噪过程的累积误差就被限制在一个更小的范围内，从而有机会用更少的步数逼近真实结果。

具体公式是：

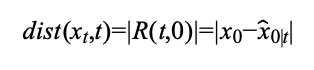
该公式量化了在当前时刻距离真实数据的距离，不仅是当前的估计误差，更是所需的最小化的误差上界。

2、图论松弛压缩路径，最小化误差上界。

基于第一步的理论，ShortDF采取了激进且高效的策略：

直接将初始单步去噪路径视为“潜在的最优路径”，并通过图论松弛策略强迫模型压缩路径，从而最小化这个初始误差上界 。

核心逻辑是让模型不再盲目迭代，而是利用图论松弛（Relaxation）来判断：

是否可以通过中间节点k找到一条“捷径”，使得累积误差小于当前的直连误差？如果有，则更新路径。

这一过程本质上是在不断压低第一步中定义的误差上界，实现物理意义上的路径压缩。

关键公式1：量化代价

关键公式2：松弛判断

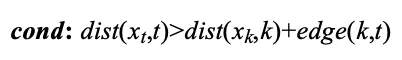
关键公式3：优化目标

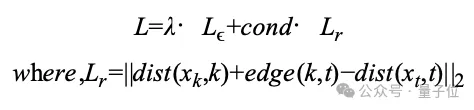
随着训练的进行，模型逐渐学会以伪递归的方式自我修正，最终实现去噪路径的全局最优。

3、多状态模型协同，确保训练稳定。

理论虽然完美，但在充满随机噪声的扩散过程中，直接进行图优化极易导致训练震荡。

为了确保优化的收敛性与稳定性，ShortDF还设计了精妙的“多状态优化（Multi-State Optimization）”。

主要通过维护三个不同角色的模型副本，分别负责预测、稳定评估和全局规划，解决了随机噪声干扰下图构建困难的问题。

具体来说：

△ShortDFv.s.图论关系和图引导的训练策略关系

硬核实战：SOTA 级的性能表现

作为CVPR Highlight工作，ShortDF在不同难度的数据集上均展现了优异的性能-速度平衡。

首先是极速推理验证，在标准基准CIFAR-10上，ShortDF展现了极致的加速能力：

• 速度跨越：仅需2步即可完成高质量生成，相比DDIM的10步基准，推理速度提升5.0倍 。
• 画质提升：2步设置FID 9.08，显著优于DDIM 10步的11.14，画质FID提升18.5%。

而对于复杂场景的鲁棒性，ShortDF在更高分辨率的CelebA（人脸）和Churches（建筑）数据集上证明了其泛化能力：

• 人脸生成：在10步推理下，ShortDF的FID降至5.0，不仅远超DDIM(10.59)，甚至优于DPM-Solver和DEIS等专用加速算法。
• 场景还原：实验表明，ShortDF在8步生成的教堂图像质量，在视觉细节上已能媲美DDIM 15步的效果，在保证画质的前提下显著减少了计算量 。

其中可视化结果显示，在相同的去噪时间节点（step是time node）上，ShortDF能更快地还原物体轮廓（如教堂尖顶、人脸五官），验证了“最短路径”理论在复杂分布下的有效性。

总的来说，ShortDF的提出，不仅在理论上首次建立了残差传播与图论最短路的数学联系，更在工程层面提供了一套具有普适性的高效解决方案。

这项工作给业界的启示在于：单纯的“算力堆砌”并非长久之计，精细化的数学建模才是打破扩散模型速度枷锁的关键钥匙。

这对于推动AIGC技术在移动端设备、实时交互设计等资源受限场景下的落地，无疑具有重要的里程碑意义。

从半年前的ShortDF（在线/图像）到如今NeurIPS 2025 Spotlight的LeMiCa（离线/视频），可以清晰地看到一条从理论探索走向复杂应用的技术进阶之路。

对于想要深入研究这一技术路线的读者，除了重温ShortDF，也推荐关注其最新演进成果。

论文地址：https://arxiv.org/abs/2503.03265

代码地址：https://github.com/UnicomAI/ShortDF

LeMiCa地址：https://unicomai.github.io/LeMiCa

文章来自于“量子位”，作者“允中”。