新一代视觉生成范式「VAR: Visual Auto Regressive」视觉自回归来了!使 GPT 风格的自回归模型在图像生成首次超越扩散模型,并观察到与大语言模型相似的 Scaling Laws 缩放定律、Zero-shot Task
Generalization 泛化能力:

论文标题: "Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction"
这项名为 VAR 的新工作由北京大学和字节跳动的研究者提出,登上了 GitHub 和 Paperwithcode 热度榜单,并得到大量同行关注:
目前体验网站、论文、代码、模型已放出:
在自然语言处理中,以 GPT、LLaMa 系列等大语言模型为例的 Autoregressive 自回归模型已经取得了较大的成功,尤其 Scaling Law 缩放定律和 Zero-shot Task Generalizability 零样本任务泛化能力十
分亮眼,初步展示出通往「通用人工智能 AGI」的潜力。
然而在图像生成领域中,自回归模型却广泛落后于扩散(Diffusion)模型:近期持续刷屏的 DALL-E3、Stable Diffusion3、SORA 等模型均属于 Diffusion 家族。此外,对于视觉生成领域是否存在
「Scaling Law 缩放定律」仍未知,即测试集损失是否随模型或训练开销增长而呈现出可预测的幂律 (Power-law) 下降趋势仍待探索。
GPT 形式自回归模型的强大能力与 Scaling Law,在图像生成领域,似乎被「锁」住了:

自回归模型在生成效果榜单上落后于一众 Diffusion 模型
剑指「解锁」自回归模型的能力和 Scaling Laws,研究团队从图像模态内在本质出发,模仿人类处理图像的逻辑顺序,提出一套全新的「视觉自回归」生成范式:VAR, Visual AutoRegressive Modeling,
首次使得 GPT 风格的自回归视觉生成,在效果、速度、Scaling 能力多方面超越 Diffusion,并迎来了视觉生成领域的 Scaling Laws:

VAR 方法核心:模仿人类视觉,重新定义图像自回归顺序
人类在感知图像或进行绘画时,往往先概览全局、再深入细节。这种由粗到细、从把握整体到精调局部的思想非常自然:
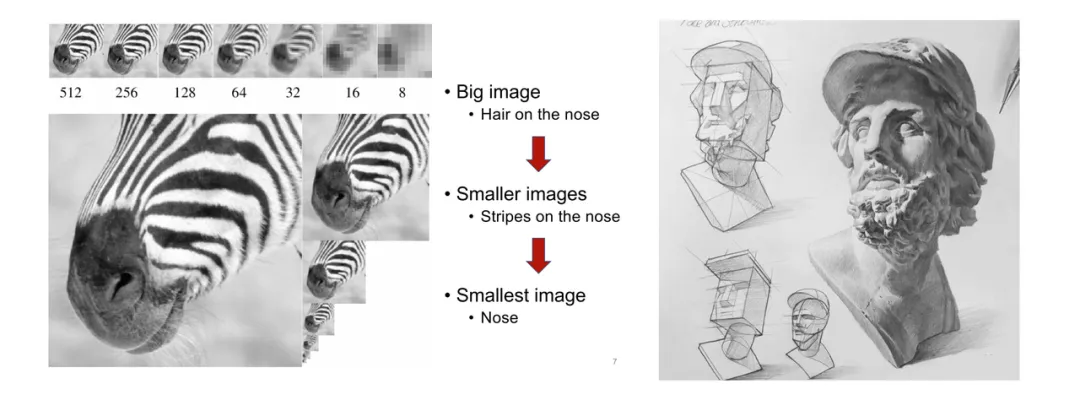
人类感知图片(左)与创作画作(右)由粗到细的逻辑顺序
然而,传统的图像自回归(AR)却使用一种不符合人类直觉(但适合计算机处理)的顺序,即自上而下、逐行扫描的光栅顺序(或称 raster-scan 顺序),来逐个预测图像 token:

VAR 则「以人为本」,模仿人感知或人创造图像的逻辑顺序,使用从整体到细节的多尺度顺序逐渐生成 token map:
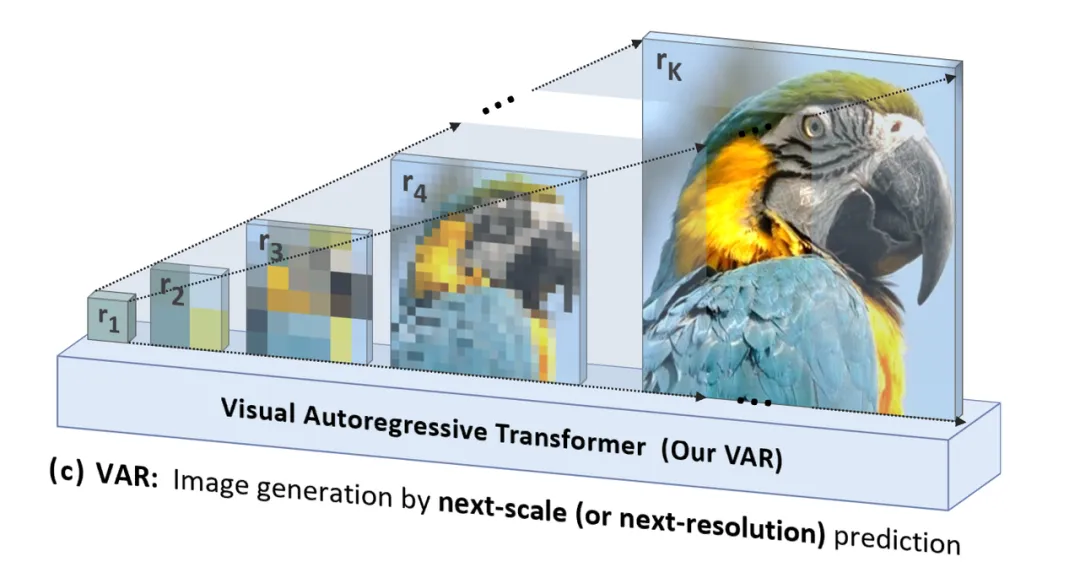
除了更自然、更符合人类直觉,VAR 带来的另一个显著优势是大幅提高了生成速度:在自回归的每一步(每一个尺度内部),所有图像 token 是一次性并行生成的;跨尺度则是自回归的。这使得在模型参
数和图片尺寸相当的情况下,VAR 能比传统 AR 快数十倍。此外,在实验中作者也观察到 VAR 相比 AR 展现出更强的性能和 Scaling 能力。

VAR 在第一阶段训练一个多尺度量化自动编码器(Multi-scale VQVAE),在第二阶段训练一个与 GPT-2 结构一致(结合使用 AdaLN)的自回归 Transformer。
如左图所示,VQVAE 的训练前传细节如下:
如右图所示,在 VQVAE 训练结束后,会进行第二阶段的自回归 Transformer 训练:
作者表示,VAR 的自回归框架是全新的,而具体技术方面则吸收了 RQ-VAE 的残差 VAE、StyleGAN 与 DiT 的 AdaLN、PGGAN 的 progressive training 等一系列经典技术的长处。VAR 实际是站在巨人的
肩膀上,聚焦于自回归算法本身的创新。
VAR 在 Conditional ImageNet 256x256 和 512x512 上进行实验:
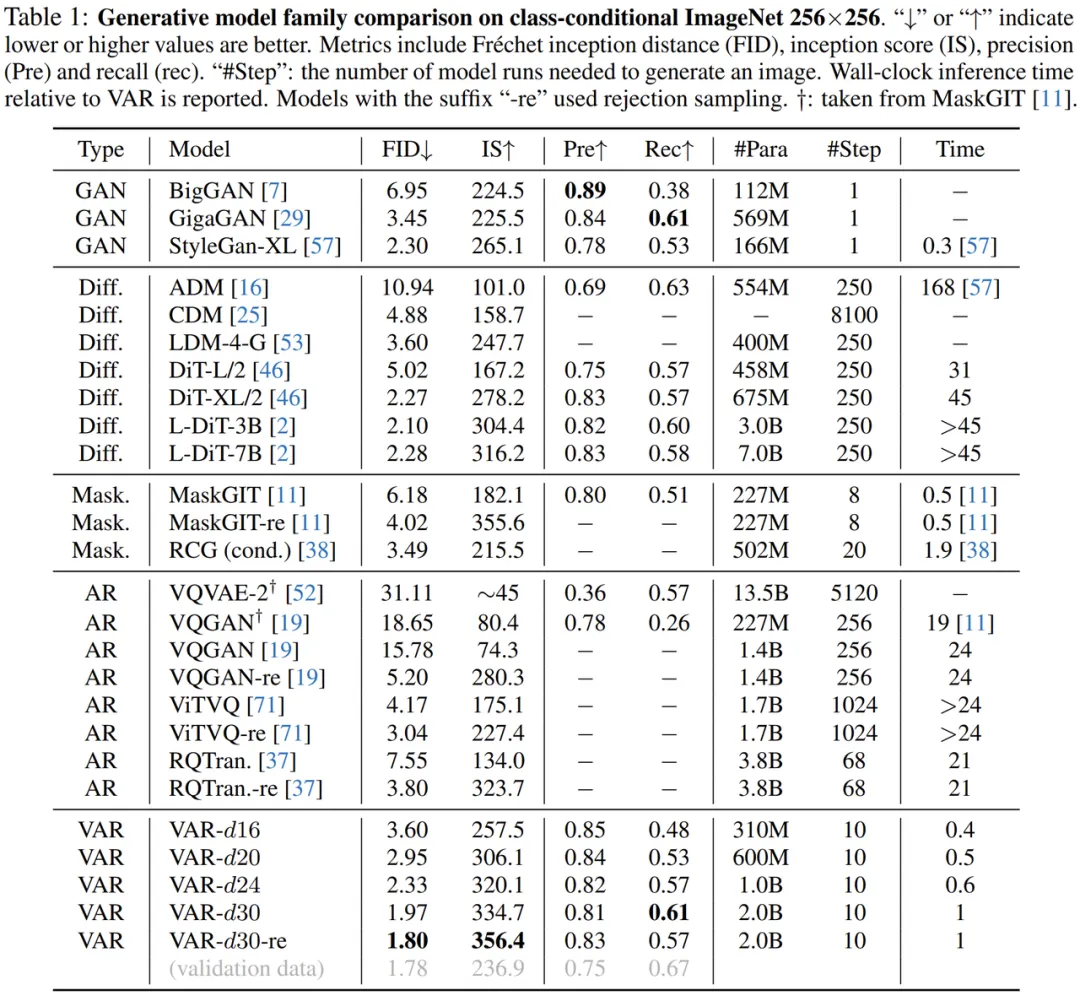
令人关注的是,通过与 SORA、Stable Diffusion 3 的基石模型 Diffusion Transformer(DiT)对比,VAR 展现出了:
这些比 DiT 更高效、更高速、更可扩放的证据为新一代视觉生成的基础架构路径带来了更多可能性。

Scaling Law 实验
Scaling law 可谓是大语言模型的「皇冠明珠」。相关研究已经确定,在 Scale up 自回归大型语言模型过程中,测试集上的交叉熵损失 L,会随着模型参数量 N、训练 token 个数 T,以及计算开销 Cmin 进
行可预测的降低,呈现出幂律(Power-law)关系。
Scaling law 不仅使根据小模型预测大模型性能成为可能,节省了计算开销和资源分配,也体现出自回归 AR 模型强大的学习能力,测试集性能随着 N、T、Cmin 增长。
通过实验,研究者观察到了 VAR 展现出与 LLM 几乎完全一致的幂律 Scaling Law:研究者训练了 12 种大小的模型,缩放模型参数量从 1800 万到 20 亿,总计算量横跨 6 个数量级,最大总 token 数达到
3050 亿,并观察到测试集损失 L 或测试集错误率 与 N 之间、L 与 Cmin 之间展现出平滑的的幂律关系,并拟合良好:
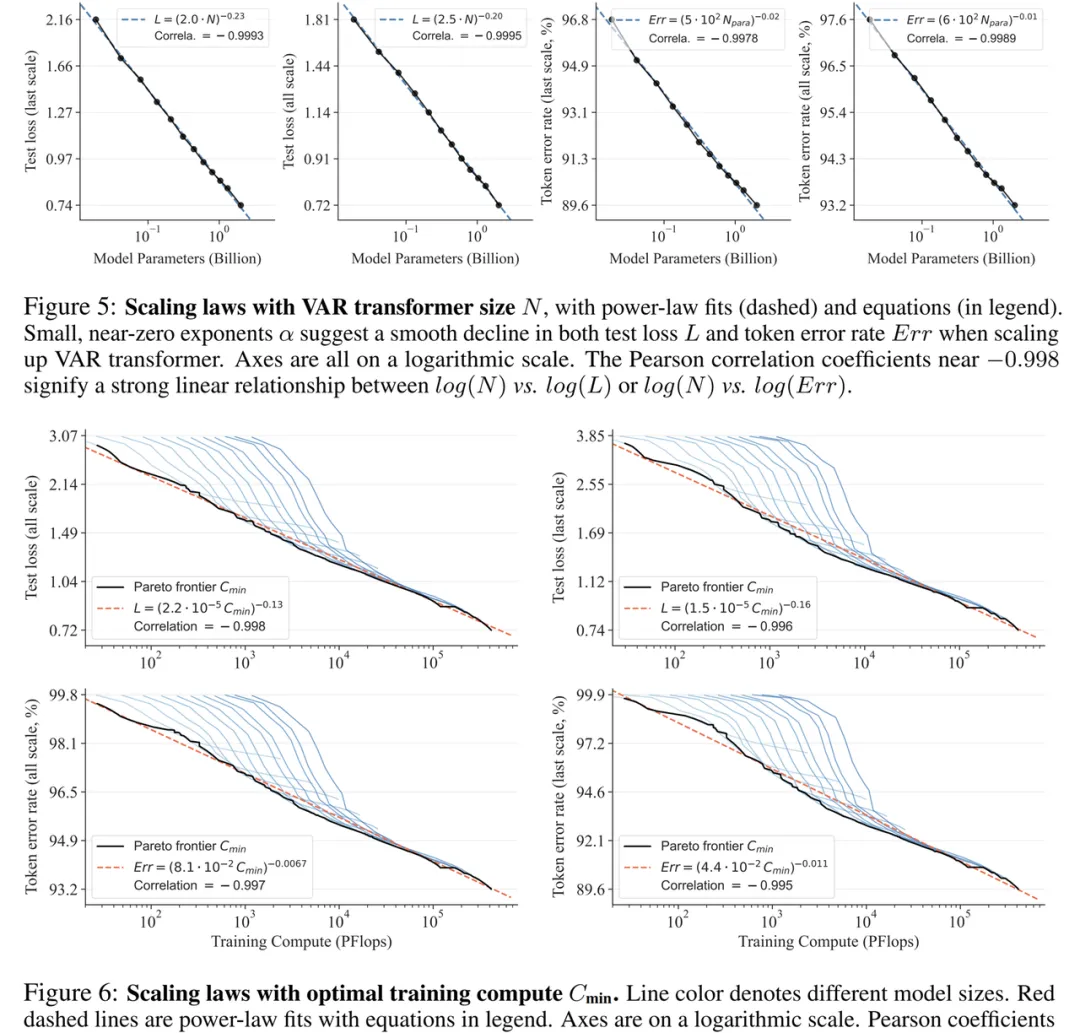
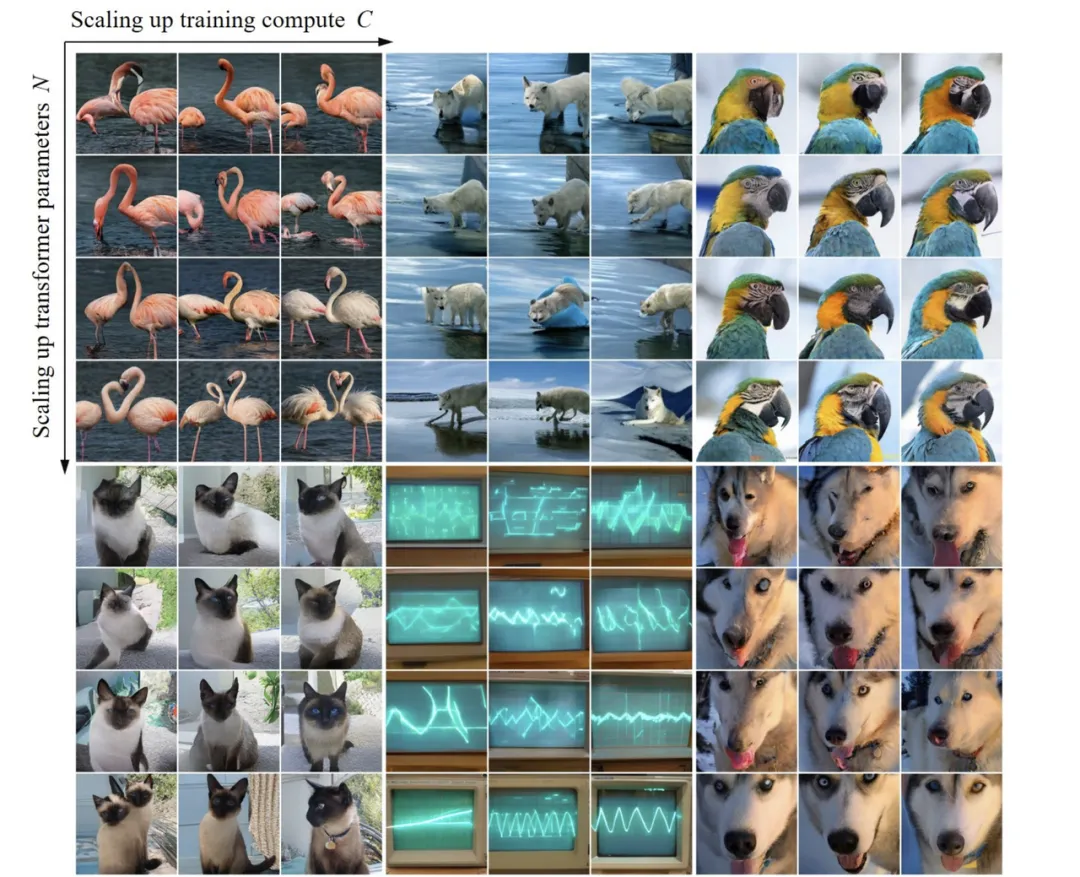
在 scale-up 模型参数和计算量过程中,模型的生成能力可见得到逐步提升(例如下方示波器条纹):
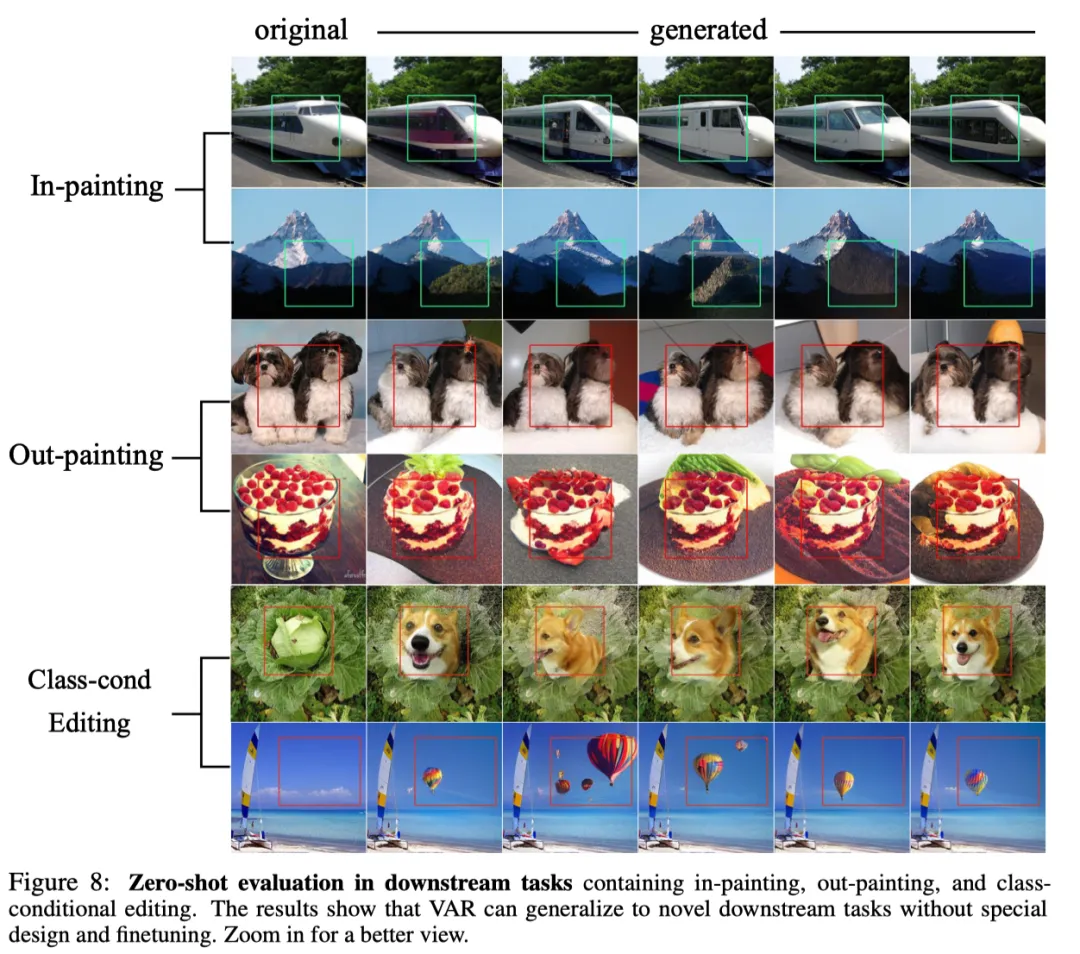
得益于自回归模型能够使用 Teacher-forcing 机制强行指定部分 token 不变的这一优良性质,VAR 也展现出一定的零样本任务泛化能力。在条件生成任务上训练好的 VAR Transformer,不通过任何微调即可
零样本泛化到一些生成式任务中,例如图像补全(inpainting)、图像外插(outpainting)、图像编辑(class-condition editing),并取得一定效果:
VAR 为如何定义图像的自回归顺序提供了一个全新的视角,即由粗到细、由全局轮廓到局部精调的顺序。在符合直觉的同时,这样的自回归算法带来了很好的效果:VAR 显著提升自回归模型的速度和生成
质量,在多方面使得自回归模型首次超越扩散模型。同时 VAR 展现出类似 LLM 的 Scaling Laws、Zero-shot Generalizability。作者们希望 VAR 的思想、实验结论、开源,能够贡献社区探索自回归范式在
图像生成领域的使用,并促进未来基于自回归的统一多模态算法的发展。
文章来自微信公众号“机器之心”,作者:机器之心编辑部
