Sora刚发布后没多久,火眼金睛的网友们就发现了不少bug,比如模型对物理世界知之甚少,小狗在走路的时候,两条前腿就出现了交错问题,让人非常出戏。
对于生成视频的真实感来说,物体的交互非常重要,但目前来说,合成真实3D物体在交互中的动态行为仍然非常困难。
与无条件或文本条件的动力学不同的是,以动作为条件的动力学(action-conditioned dynamics)需要感知对象的物理材料属性,并将3D运动预测建立在这些属性(例如物体刚度)的基础上。
但由于缺乏材料的真实数据,估计物理材料属性仍然是一个悬而未决的问题,因为测量真实物体的物理材料属性非常困难。
最近,来自MIT、斯坦福大学、哥伦比亚大学和康奈尔大学联合提出了一种基于物理的方法模型PhysDreamer,利用视频生成模型学习到的对象动力学先验,为静态3D对象赋予交互式动力学。

论文链接:https://arxiv.org/pdf/2404.13026.pdf
项目主页:https://physdreamer.github.io/
通过提炼上述先验知识,PhysDreamer 能够合成现实物体对全新交互的响应,例如外力或智能体操作,并且通过在弹性物体的不同示例上展现了该方法的效果,利用用户研究评估了合成交互的真实性。
给定一个由3D高斯表示的静态物体(其中xp表示位置,αp表示不透明度,Σp表示协方差矩阵,cp表示粒子的颜色),最终目标是估计对象的物理材料属性场,以实现真实的交互式运动合成。
具体性质包括质量m、杨氏模量E和泊松比ν,其中杨氏模量用来测量材料的刚度,决定物体响应外力作用的运动轨迹:较高的杨氏模量会带来更小的形变,以及更刚性和更高频率的运动。

所以研究人员将问题形式化为,估计3D物体的空间变化杨氏模量场E(x),可以用查询粒子的杨氏模量,以进行粒子模拟。
至于其他物理性质,粒子的质量m_p可以预先计算为恒定密度(ρ)和粒子体积Vp的乘积;粒子体积可以通过将「背景单元的体积」除以「该单元包含的粒子数」来估计得到;泊松比νp对物体运动的影响可以忽略不计,可以假设为常数。
PhysDreamer可以估计静态3D对象的材质场,其关键想法在于生成运动中物体的可信视频,然后优化材料场E(x)以匹配合成运动。
给定一个表示为3D高斯的对象,首先从某个视点进行渲染(带背景),然后使用图像到视频生成模型来生成运动中物体的参考视频,再使用可微分材质点方法(MPM,Material Point Methods)和可微分渲染,对空间变化的材质场和初始速度场进行优化,旨在最小化渲染视频和参考视频之间的差异。
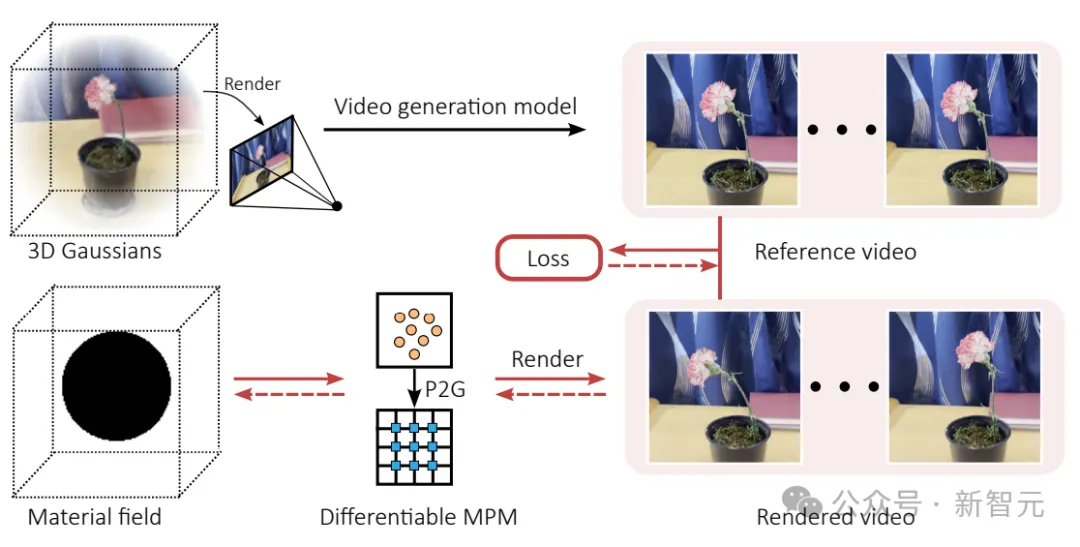
3D高斯采用一组各向异性的3D高斯核来表示3D场景的辐射场,虽然其主要是作为3D新视图合成方法引入的,但由于3D高斯具有拉格朗日性质,所以能够直接适用于粒子的物理模拟器。
与PhysGaussian方法类似,研究人员使用材质点方法(MPM,Material Point Methods)直接在高斯粒子上模拟物体动力学。
由于3D高斯分布主要位于物体表面,因此可以应用可选的内部填充过程来提高模拟真实感。
在连续介质力学中,材料的变形是通过一个映射函数ϕ来进行模拟的,可以将材料在未变形状态下的空间点X转换为变形后的世界空间中的点x,这个过程可以用公式
为了衡量材料变形中的局部旋转和应变(strain),引入了形变梯度(deformation gradient)的概念,为映射函数ϕ的雅可比矩阵F,即
形变梯度是理解和描述材料应力-应变关系的关键,涉及到材料的局部变形状态。
在高弹性材料中,Cauchy应力(stress)的计算依赖于应变能密度函数ψ(F),可以对材料非刚性变形的程度进行量化;通常来说,该函数由材料科学家根据材料的对称性和旋转不变性原则设计,并与实验数据相匹配。
此外,固定旋转超弹性模型中的能量密度函数可以通过变形梯度的一个奇异值σi来表示,并且模型参数μ和λ与材料的杨氏模量E和泊松比ν有直接关系,这些参数对于理解材料在受力时的表现至关重要。

研究人员使用移动最小二乘材料点法(MLS-MPM)来求解「弹性材料动态」的控制方程,其中ρ代表密度,v(x, t)代表世界空间的速度场,f代表外部力。
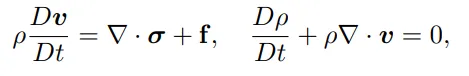
MPM是一种用于模拟各种材料动力学的计算方法,结合了欧拉和拉格朗日方法的优点,特别适合于模拟固体、流体、沙子、布料等材料的动态行为,能够有效处理材料的拓扑变化,并且在图形处理单元(GPU)上容易实现并行化。
通过将物体视为一系列高斯粒子来进行空间离散化,每个粒子p代表物体的一小部分体积,并携带体积、质量、位置、速度、变形梯度和局部速度场梯度等属性。
MPM的计算过程包括粒子到网格(P2G)和网格到粒子(G2P)的转换循环(transfer loop):
在P2G阶段,动量从粒子传递到网格,更新网格上的速度,然后这些更新后的速度信息被传回粒子,用于更新粒子的位置和速度,同时,粒子的局部速度梯度和变形梯度也会相应更新,以反映材料的当前状态。
MPM方法可以对材料的复杂动态行为进行精确模拟,包括材料的变形、断裂和交互作用。
研究人员使用移动最小二乘材质点法(MLS-MPM)作为物理仿真器,并采用固定旋转超弹性材料模型来模拟三维物体的过程。
仿真器使用MLS-MPM来模拟物体的物理行为,仿真函数接收当前时间步t的粒子位置x、速度v、形变梯度F和局部速度场梯度C,以及粒子的物理属性集合θ(包含所有粒子的质量、杨氏模量、泊松比和体积)和时间步长Δt(1×10^-4)作为输入,并输出下一个时间步t+1的相应值。
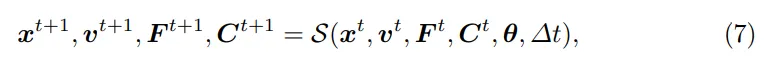
为了模拟相邻视频帧之间的动态,通常需要迭代几百个子步。
在仿真后,使用可微分渲染函数Frender来渲染每个帧的高斯粒子,其中Rt表示从仿真步骤中获得的所有粒子的旋转矩阵。
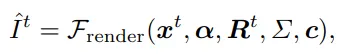
材质场和速度场通过两个三平面(triplanes)和三层多层感知器(MLP)来进行参数化,为了提升空间平滑性,对这两个场的所有空间平面应用了总变分正则化(total variation regularization)。
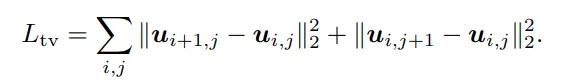
优化过程被分为两个阶段以提高稳定性和加快收敛速度:
1. 在第一阶段,对每个高斯粒子的杨氏模量进行随机初始化并固定,然后仅使用参考视频的前三个帧来优化每个粒子的初始速度。
2. 在第二阶段,固定初始速度并优化空间变化的杨氏模量。为了防止梯度爆炸或消失,梯度信号只流向前一帧。
通过这种方式,仿真器能够模拟物体的物理行为,并根据参考视频优化材料属性和初始条件,以生成逼真的动态效果。
3. 用子采样(subsampling)加速模拟
使用三维高斯粒子进行高保真渲染通常需要数百万个粒子才能表示出一个场景,给运行模拟带来了巨大的计算负担。
为了提高效率,模型引入了一个子采样过程,在大大减少计算量的同时,还能保持渲染结果的高保真度:只用少量的驱动粒子(driving particle)进行模拟,然后通过插值驱动粒子来获得高斯粒子的位置和旋转,有效地平衡了计算效率和渲染质量。
具体来说,模型使用K-Means聚类算法在t=0时刻创建一组驱动粒子,其中每个驱动粒子由一组物理属性表示,包括位置、速度、形变梯度、局部速度场梯度、杨氏模量、质量、泊松比和体积。
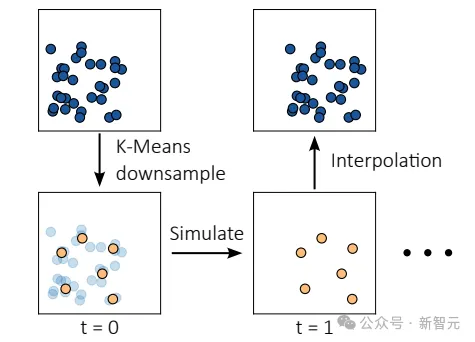
驱动粒子的初始位置是其所有聚类成员位置的平均值,其中驱动粒子的数量远小于三维高斯粒子的数量。
在渲染过程中,通过插值驱动粒子的位置和旋转来计算每个三维高斯粒子的位置和旋转:对于每个三维高斯粒子,首先找到它在t=0时刻的八个最近邻驱动粒子,然后拟合这些八个驱动粒子在t=0时刻和当前时间戳之间的刚体变换T,以确定粒子的当前位置和旋转。
数据集
通过捕捉多视角图像,研究人员收集了八个真实世界的静态场景,其中每个场景包括一个物体和一个背景,物品包括五朵花(一朵红玫瑰、一朵康乃馨、一朵橙玫瑰、一朵郁金香和一朵白玫瑰)、一株海芋、一根电话线和一顶无檐帽;然后捕捉四个交互视频来说明其在交互后的自然运动,例如戳或拖,再使用真实视频作为额外的对比参考。
实验结果

在用户研究中,与基线方法和真实世界捕捉的视频对比后可以看到,有超过80%的参与者在两项选择实验(2AFC)中更倾向于PhysDreamer模型,认为其在运动的真实性上更胜一筹;在视觉质量方面,也有65%的参与者更偏好PhysDreamer
需要注意的是,由于比较的静态场景本身是一致的,因此视觉质量的评估也在一定程度上也依赖于生成物体的运动效果。

从运动模式在不同时间点上的切片中可以观察到,PhysGaussian由于缺少对材料属性进行原理性估计,导致其生成的运动幅度过大且速度过慢,与现实不符。
而与DreamGaussian4D相比,有70%和63.5%的2AFC样本在视觉质量和运动真实性上更倾向于PhysDreamer模型,从上图中可以看到,DreamGaussian4D生成的运动是周期性的,且幅度保持在一个较小的恒定值,相比之下,PhysDreamer能够模拟出运动中的衰减效果。
本文来自微信公众号“新智元”

【开源免费】Browser-use 是一个用户AI代理直接可以控制浏览器的工具。它能够让AI 自动执行浏览器中的各种任务,如比较价格、添加购物车、回复各种社交媒体等。
项目地址:https://github.com/browser-use/browser-use
【开源免费】AutoGPT是一个允许用户创建和运行智能体的(AI Agents)项目。用户创建的智能体能够自动执行各种任务,从而让AI有步骤的去解决实际问题。
项目地址:https://github.com/Significant-Gravitas/AutoGPT
【开源免费】MetaGPT是一个“软件开发公司”的智能体项目,只需要输入一句话的老板需求,MetaGPT即可输出用户故事 / 竞品分析 / 需求 / 数据结构 / APIs / 文件等软件开发的相关内容。MetaGPT内置了各种AI角色,包括产品经理 / 架构师 / 项目经理 / 工程师,MetaGPT提供了一个精心调配的软件公司研发全过程的SOP。
项目地址:https://github.com/geekan/MetaGPT/blob/main/docs/README_CN.md