最近一周KAN的热度逐渐褪去，正好静下心来仔细学习KAN的原理，收获颇多。

KAN是一种全新的神经网络架构，它与传统的MLP架构不同，能够用更少的参数量在Science领域取得惊人的表现，并且具备可解释性，有望成为深度学习模型发展的一个重要方向。

运用KAN，我们不仅能够在函数拟合、偏微分方程求解（PDE）上取得不错的成果，甚至能够解决拓扑理论中的Knot Theory、处理凝聚态物理中的Anderson Localization问题。

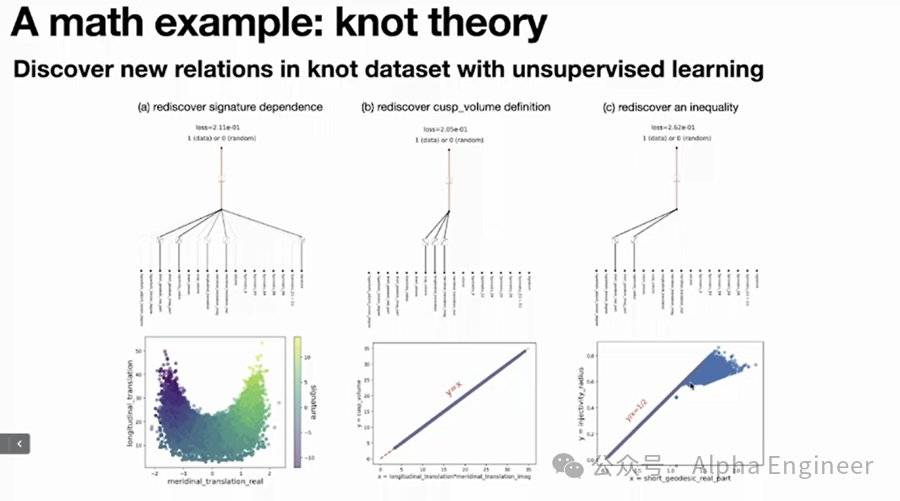
KAN一经推出便引爆了整个AI圈，短短几天就在github上获得了10k以上的stars。各路大神蜂拥而至，对KAN做出多种改进，提出了EfficientKAN、FourierKAN，甚至Kansformer等全新架构。

那么KAN究竟是什么，它有哪些独特价值，它对未来AI发展又有哪些启发呢？

近期KAN论文的一作Ziming做了一场精彩的分享，从数学原理、模型性能、甚至哲学意义层面对KAN的价值进行了深入解析，信息量巨大。

我给大家解读一下这场讲座的精华内容，感兴趣的朋友也可以去亲自听一遍。

文章内容有点硬核，建议耐心阅读哈。相信看完这篇文章，你对KAN以及深度学习模型的未来，会有一个全新的认知。

一、KAN的数学原理：KART定理

KAN的全称是Kolmogorov–Arnold Network，致敬了两位伟大的已故数学家，其背后的核心思想是Kolmogorov–Arnold表示定理，即KART（Kolmogorov–Arnold Representation Theorem）。

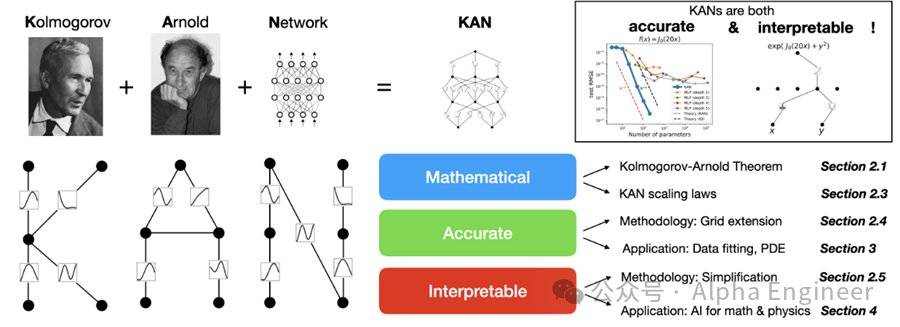
KART的核心思想是：对于任何一个多元连续函数，都能够表示为有限个单变量函数和加法的组合。

数学定理读起来比较拗口，但如果把它图示化出来，就很容易弄懂。

假设有一个多元连续函数y=f(x1,x2)，它可以表达为一个有着2个input（x1和x2）、一个output（y）、以及5个隐藏层神经元的Kolmogorov Network。隐藏层神经元数量为2n+1=5，这里的n指的是input变量的个数。

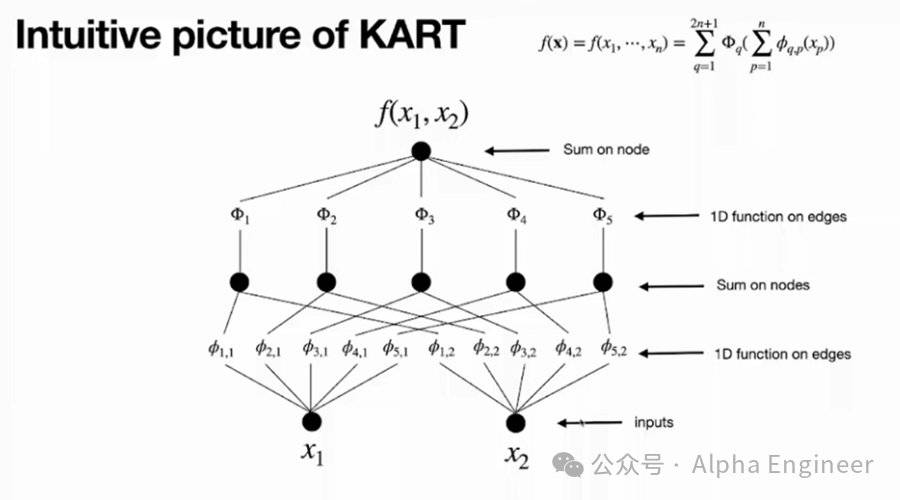
对于第一个神经元，它接收到两个branch的信号，分别是φ1,1(x1)和φ1,2(x2)，这里的φ(xi)是xi的一元函数。把φ1,1(x1)和φ1,2(x2)简单相加，就得到第一个神经元的取值。

以此类推，第2-5个神经元也是如此，这是第一层神经元取值的计算方法。

为了计算第二层神经元的结果，我们需要对第一层中的每个神经元构造一元函数（Φ1到Φ5），然后相加。

这里无论是第一层的函数（小φ）还是第二层的函数（大Φ），都是一元函数，所以可以用曲线将其可视化地表达出来。

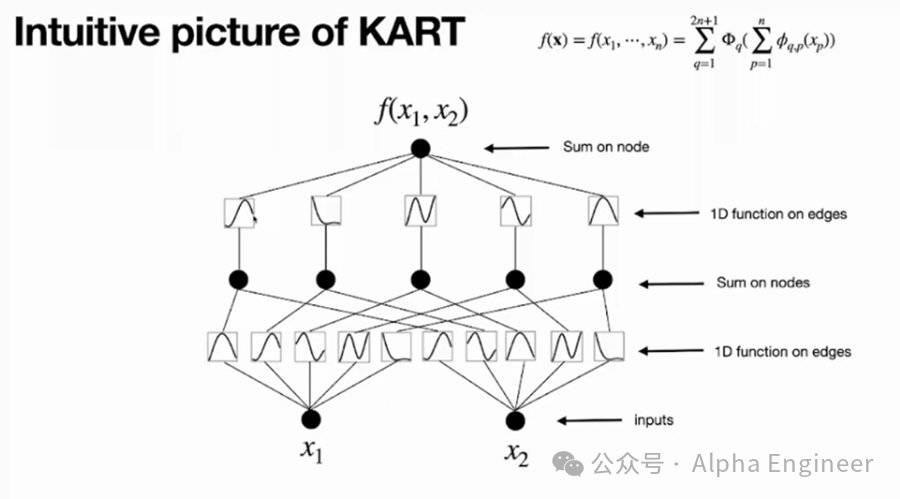
至此，我们将f(x1,x2)的KART表示，转化成了一个两层KAN网络，并且进行了可视化。

二、将KAN网络做得更深：Make it deeper

原始的Kolmogorov Network特指一个2层的，宽度是2n+1的网络（其中n代表输入变量个数），第一层的小φ被称为内部函数，第二层的大Φ被称为外部函数。

这里我们可以对内部函数和外部函数进行抽象，它们都是KAN Layer，其中小φ是一个5×2的KAN Layer，大Φ是一个1×5的KAN Layer。

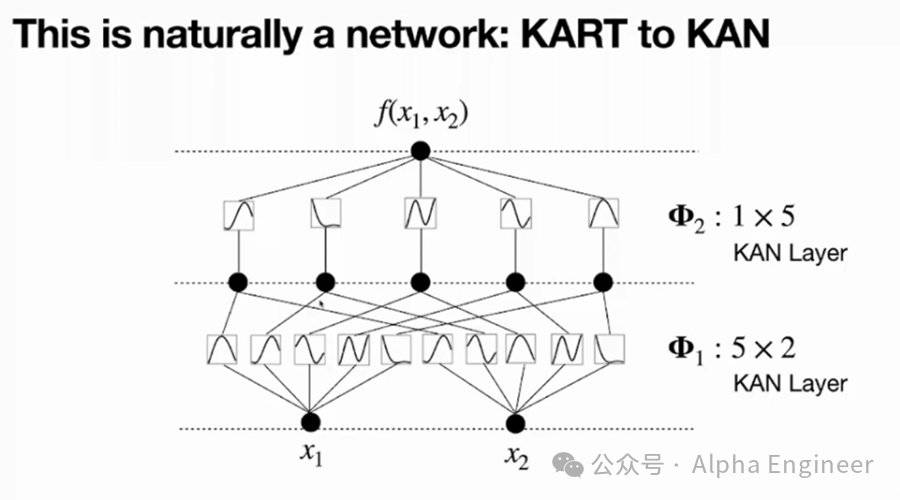
在这个基础之上，我们就可以把KAN网络建设得更深了，比如下图是一个三层的KAN。

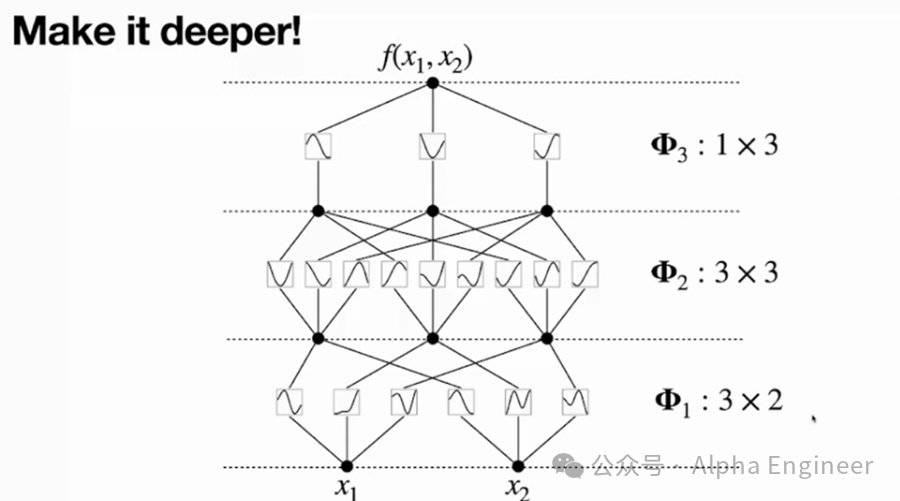
这里有一个关键的问题：如果原始的两层Kolmogorov Network就可以表示所有的光滑函数，那为什么还要把网络建深呢？

这是因为原始的两层Kolmogorov Network中，并没有约束激活函数必须为光滑函数，因此有时会求解出一些不光滑的，甚至有分形行为的病态激活函数来表达目标函数。

如果你用不光滑的函数表达了目标函数，其实是没有现实意义的，不具备预测价值。

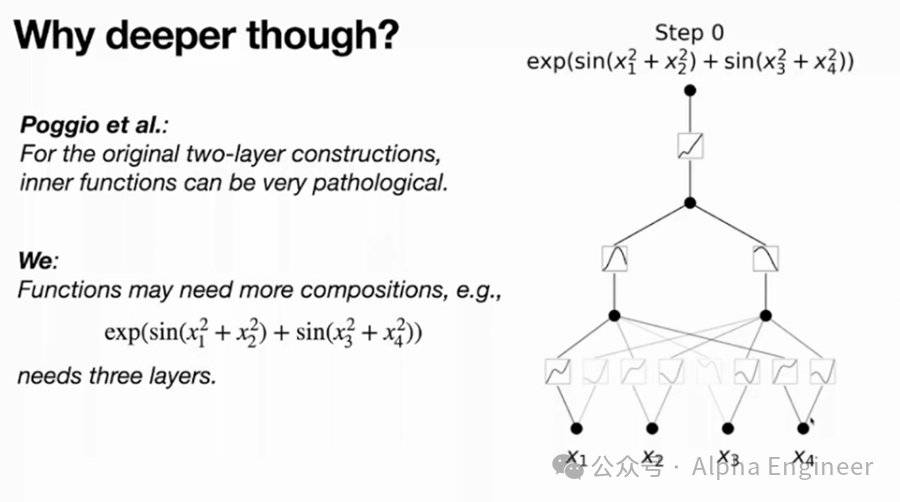
举个例子，针对这样一个目标函数，需要三层非线性的组合，才能构造出这个函数。如果用一个两层KAN网络去硬拟合，可能会得到一个没有物理意义的病态解。

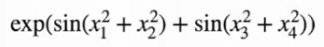
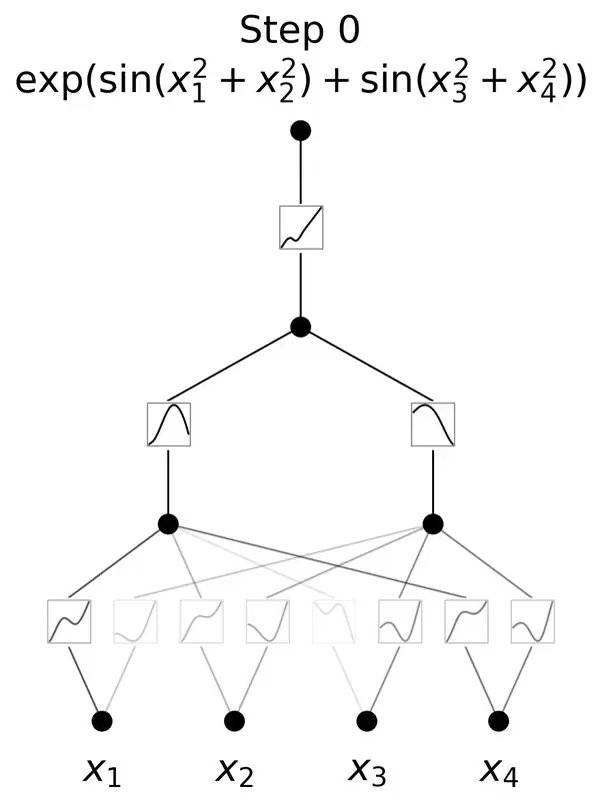
通过一个三层KAN网络，可以学习出如下结果，第一层学到了4个二次函数，第二层学到了两个sin函数，第三层学到了一个exp函数，三者通过加法组合，得到了最终的目标函数。

‘

三、用具体案例演示KAN的工作原理

上面我们用通俗的语言解释了KAN的网络架构，下面我们举几个具体例子来说明KAN的运作原理。

案例1：给定两个输入x和y，目标函数是x*y，即乘法运算。

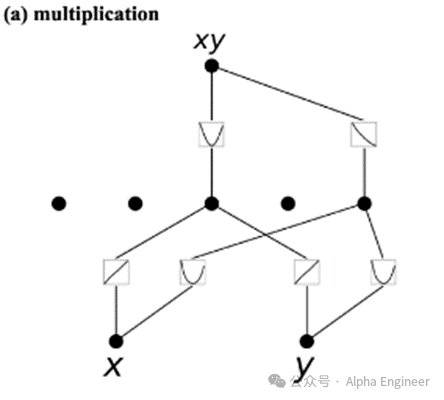
下面看一下KAN网络学到的激活函数：

第一层中，针对node1，学到两个激活函数：

φ1(x) = x

φ2(y) = y

因此node1 = φ1(x) + φ2(y) = x + y。

第一层中，针对node2，学到两个激活函数：

φ3(x) = x2

φ4(y) = y2

因此node2 = φ3(x) + φ4(y) = x2 + y2。

第二层中，学到两个激活函数：

Φ5 = node12 = (x + y)²

Φ6 = -node2 = -(x² + y²)

因此最终结果为Φ5 + Φ6 = (x + y)² - (x² + y²) = 2xy。

我们通过两层KAN网络，成功拟合出了x*y这个目标函数。

案例2：给定两个输入x和y，目标函数是x/y，即除法运算。

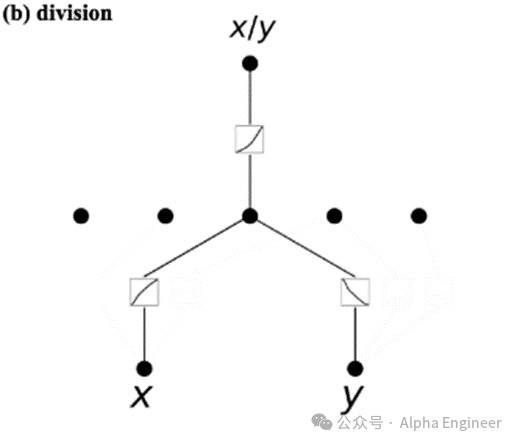
这里同样用一个两层的KAN来学习，学到的激活函数结果如下：

第一层，学到两个激活函数：

φ1(x) = log(x)

φ2(y) = -log(y)

于是node1 = φ1(x) + φ2(y) = log(x) - log(y) = log(x/y)。

第二层：

Φ3 = enode1 = elog(x/y) = x/y

于是，我们通过一个两层的KAN网络求解出了除法函数。

除了这两个简单的案例之外，作者还给出了若干有趣的函数案例。

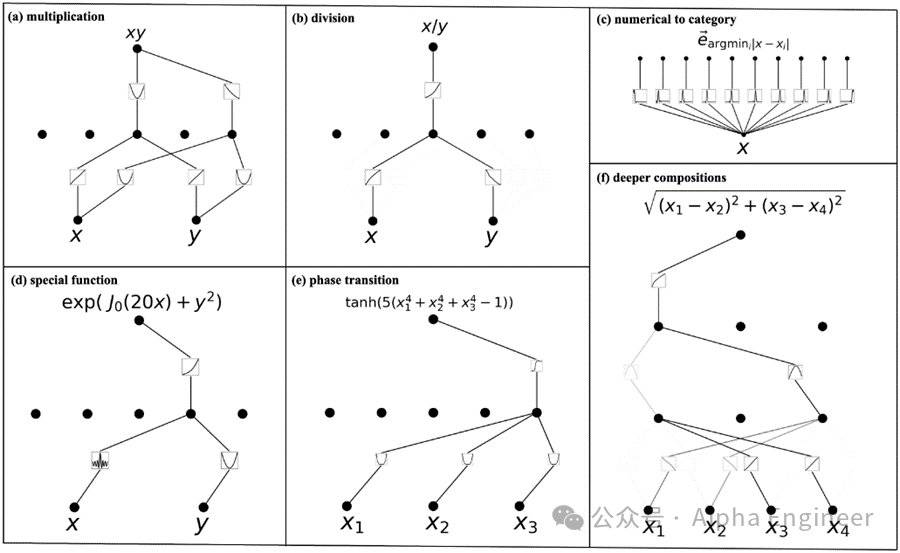
在（d）这个例子中，作者尝试用KAN来学习特殊函数，比如贝塞尔函数，结果确实学习出来了。这里的φ1(x) 是一个非常振荡的函数，就是贝塞尔函数。

在（f）这个例子中，我们想要预测两个点在二维空间中的距离函数，这时需要一个三层的KAN网络，其中包括一个线性函数、一个平方函数、一个平方根函数。三层嵌套，就能够准确拟合出目标函数。

四、KAN背后的核心算法：B-Splines

为了将Kolmogorov-Arnold表示成为一个可以学习的神经网络模型，我们需要将其参数化。

这里用到了B样条函数（B-Splines），即通过多个局域的基函数的线性组合来构成样条。

因此，KAN真正需要学习的参数，就是这里基函数前面的系数ci。

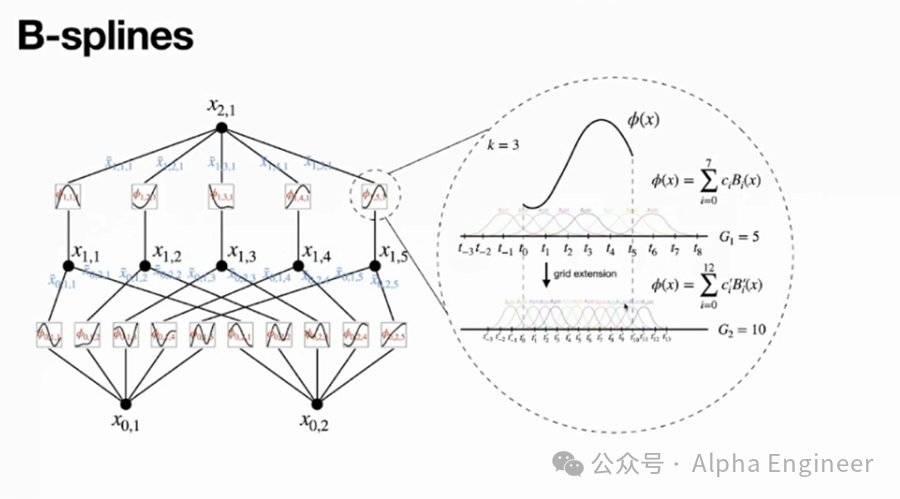
B样条函数的好处是可以自由控制resolution。比如这里G=5，意味着有5个interval，是一个比较粗糙的网格。

当G=10时便是一个比较精细的网格了。当你有更多的训练数据，想要把模型做的更精确时，你不需要重新训练网络，只需要把网格变得更细一些就可以了。

具体计算B样条函数时，常见用的是Boor Recursion Formula。这个公式表达起来很漂亮很简洁，但计算步骤存在递归性，因此计算效率较低。

这也是为什么KAN一经推出，就有大神在Github上发布EfficientKAN、FastKAN等Repo来提升其计算效率的原因。

五、KAN与MLP的关系

KAN和MLP有着千丝万缕的关系。

从数学定理方面来看，MLP的背后是万能逼近定理（Universal Approximation Theorem），即对于任意一个连续函数，都可以用一个足够深的神经网络来逼近它。

而KAN背后的数学原理是Kolmogorov-Arnold表示定理，即KART。

万能逼近定理和KART这两个表示论有一个很大的区别。

根据万能逼近定理，为了提升模型精度，需要不断提升模型的宽度。如果需要做出一个无穷精度的模型，你需要训练一个无穷宽度的网络。

而KART承诺你可以用一个有限大小的网络来实现无穷精度的模型，但有一个前提，即目标函数可以被严格写成KART的表示。

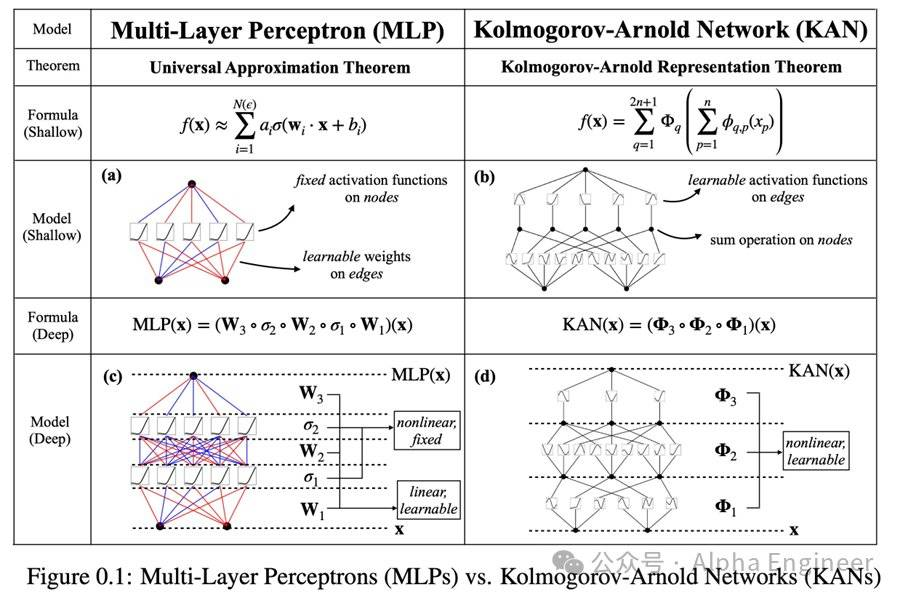
上图中的（a）和（b）比较了两层的MLP和两层的KAN。

对MLP来说，激活函数是在节点上的，是固定的。权重在边上，是可学的。

对KAN来说，激活函数是在边上的，是可学的。节点上只是一个单纯的加法，把所有input的信号加起来而已。

五、KAN在数学和物理领域具备极高的价值

下面我们来看看KAN的性能表现。

首先，对于Symbolic Formula来说，KAN的Scaling效率比MLP高了不少。

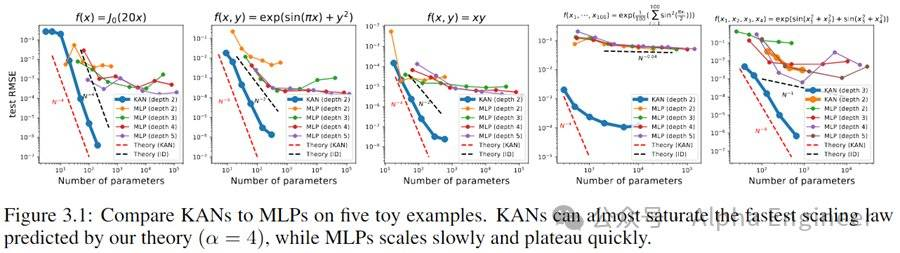
第二，在函偏微分方程求解上，KAN也比MLP更加准确。

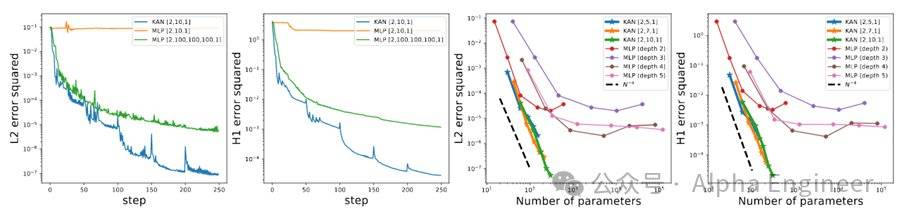
第三，与MLP不同，KAN天然具备可解释性，并且没有灾难性遗忘的风险。

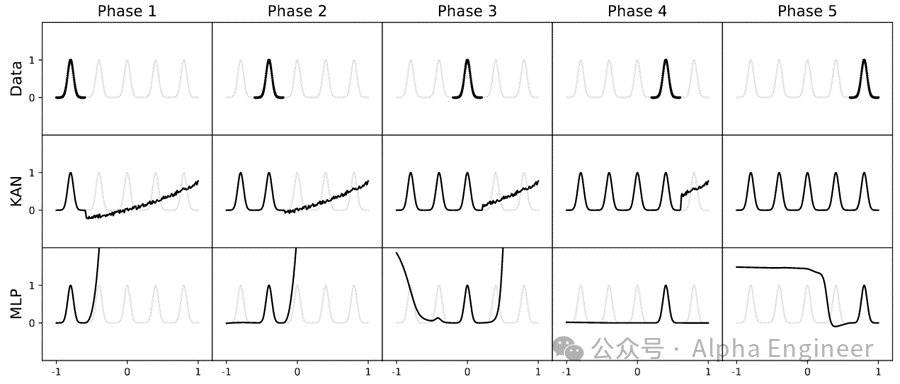
第四，人类可以与KAN进行交互，并且向其注入先验知识，从而训练出更好的模型。

这一点可能并不直观，我举个例子说明。

比如我们要预测的函数是esin(πx)+y^2。

首先我们通过KAN训练出一个比较稀疏的网络，然后prune成一个更小的网络，这时人类科学家就可以介入。

我们发现φ1长得像sin函数，于是可以把它固定成sin函数；我们觉得φ2长得像指数函数，也把它固定下来。

一旦我们将函数的structure全部固定下来后，再用KAN网络进行训练，就可以将模型中的各项参数学习到机器精度，得到一个非常准确的模型。

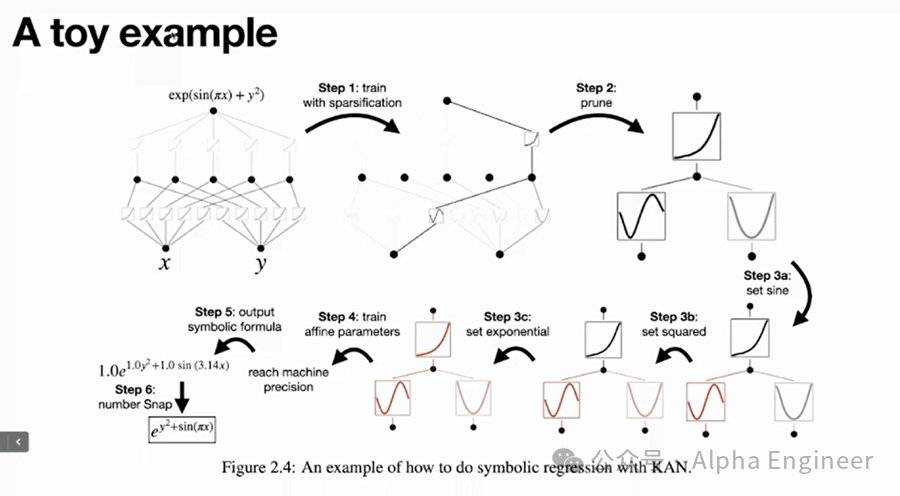
KAN是一个非常unconstrained的网络架构，它的表达能力太强，有时需要加入人类的先验知识作为constrain，才能得到更合理的结果。

七、KAN：符号主义和连接主义的桥梁

回顾AI的发展史，人们在符号主义和连接主义之间反复摇摆。

1957年，Frank Rosenblatt发明了感知机（Perceptron），人工智能正式拉开序幕。

但是在1969年，Minsky和Papert写了一本书攻击感知机，因为他们发现感知机无法执行异或操作（XOR），而XOR是计算机领域的基本操作。

这本书对Rosenblatt造成了巨大的打击，据推测间接导致其自杀。

然后时间到了1974年，政治经济学教授Paul Werbos发现，当把感知机从单层拓展到多层后，它就可以执行异或操作了。

但因为Paul Werbos所处的学术领域比较狭窄，这一发现在当时并没有引起主流学界的轰动。

1975年，Robert Hecht-Nielsen提出KART可以表示为一个层数为2、宽度为2n+1的Network，这就是KAN的雏形。

1988年，George Cybenko提出两层的Kolmogorov Network可以执行异或操作。

但是在1989年，Tomaso Poggio否定了Kolmogorov Network的价值，因为他发现两层的Kolmogorov Network解出的激活函数很不光滑，表达能力差而且没有可解释性。

时间到了2024年，Ziming和Max的研究提出了一种全新的方法，将Kolmogorov Network拓展到多层，能够有效解决激活函数不光滑的问题。

可以说，KAN是一个处于Symbolism和Connectionism之间的存在，有可能成为连接符号主义和连接主义之间的桥梁。

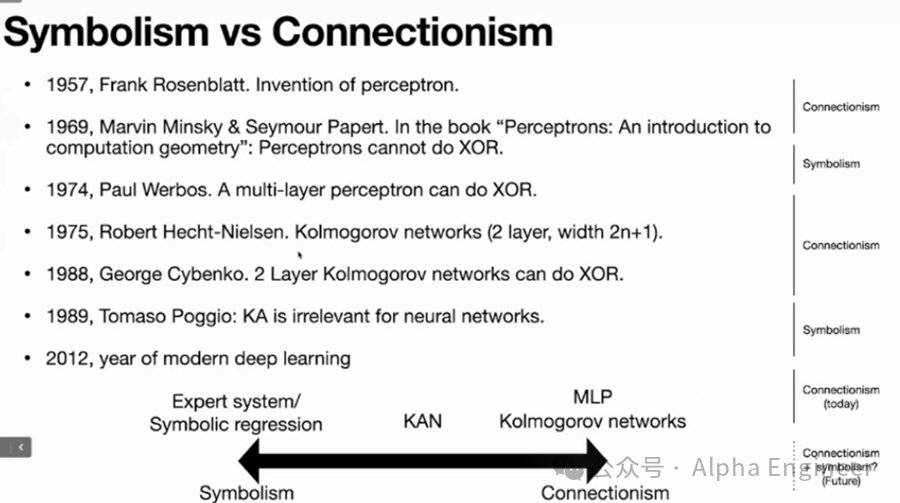
从这个意义上来看，KAN的价值就不只局限于AI for Science了。

比如最近大家在争论Sora到底是不是世界模型，有没有通过海量视频数据学到物理学规律。

要回答这个问题，可能我们就需要构建一个同时具备符号主义和连接主义的模型，两个部分各自学习自己擅长的部分。

最后我们可以去模型的Symbolism的部分去检验Sora有没有真的学到物理学规律，而不是去看整个Network，因为Connectionism部分是不可解释的。

八、KAN的哲学意义：还原论还是整体论？

从哲学的角度看，KAN的背后是还原论，而MLP的背后是整体论。

为了理解二者的差别，我们得先理解事物的内在自由度和外在自由度。

比如基本粒子存在诸如“自旋”等内在自由度，而外在自由度指的是基本粒子是如何与其他粒子发生交互的。

再比如在社会学中，如何看待一个人。从内在自由度来看，人是由他的品性、品格所决定的，这是internal degrees of freedom。

同时你也可以从外在自由度的角度去定义一个人，人是他所有社会关系的总和。

这恰恰就是KAN和MLP之间的本质差别。

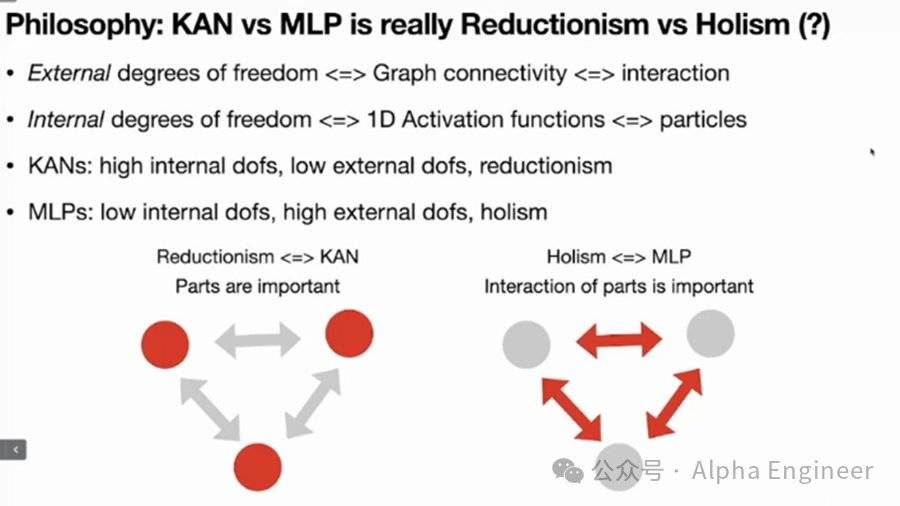
MLP不在意内在自由度，而是重视外部连接，每个神经元内部不需要做精巧的结构设计，而是用固定的激活函数。只要神经元之间的连接足够复杂，就会涌现出智能。

而KAN的逻辑是，我们需要关注内在结构，引入可学的激活函数。在引入内在结构复杂性的同时，KAN在外部连接上只有简单的加法。

MLP和KAN的背后，反映出的是还原论和整体论之间的差异。

还原论（Reductionism）认为，我们最终能够把复杂的世界拆分成基本单元，这些基本单元的内部是复杂的，但是其外部相互作用是简单的。

而整体论（Holism）则认为世界是无法拆分的，它work as a whole。

这也从另一个层面说明了为什么KAN在Science领域表现得更好。因为绝大部分科学家，都是基于Reductionism的哲学信仰在解构这个世界。

九、结语：KAN属于仿生吗？

我们知道，当前的深度神经网络模型，启发自人脑中的神经元结构。

Transformer中的Attention机制，也启发自心理学中的注意力分配原理。

仿生路线成为了目前AI领域公认的主流方向。

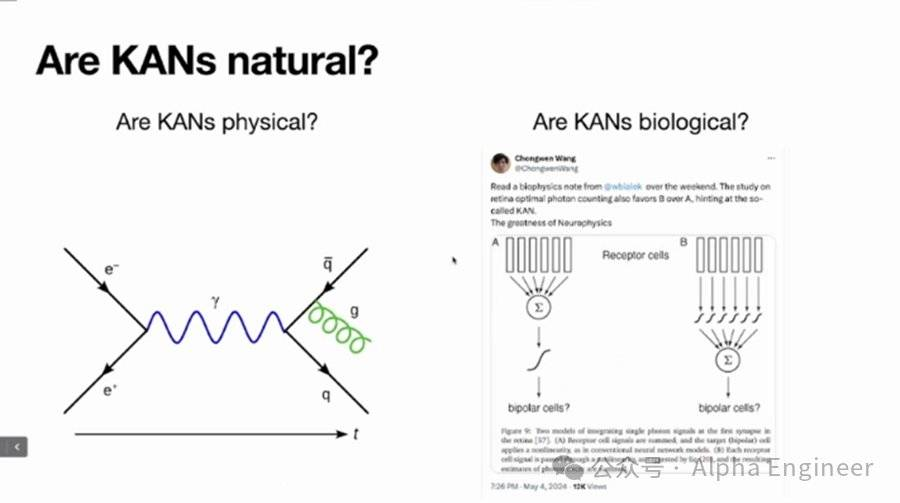
那么在大自然中，是否存在着类似KAN这样的神经网络结构呢？

答案是肯定的。

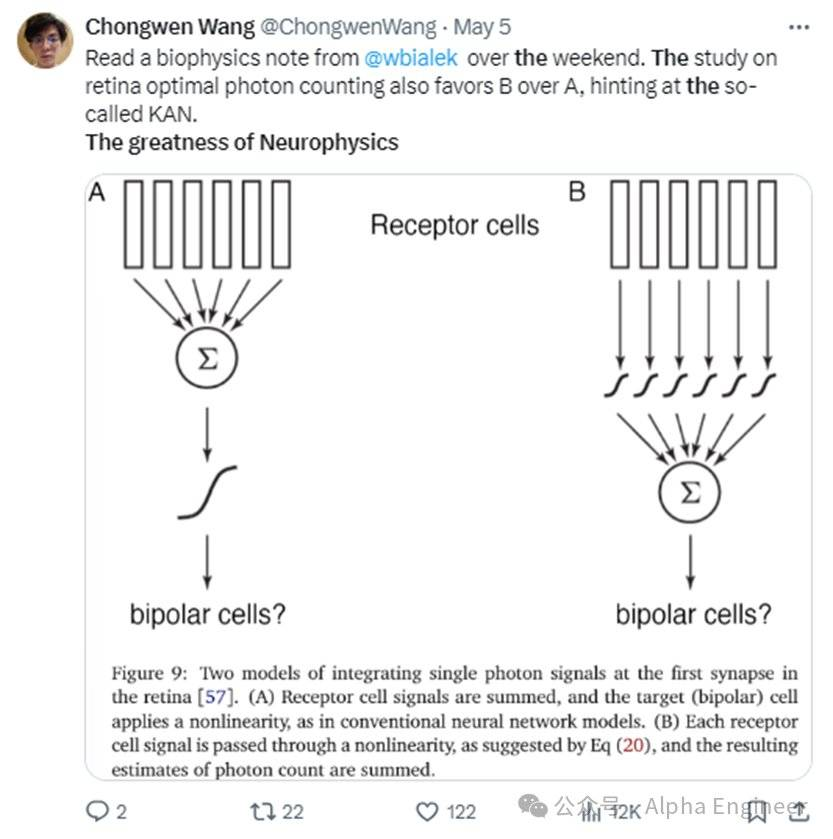
KAN论文发布后，有生物物理领域的专家提出：MLP更像大脑中的神经元，而KAN更像视网膜中的神经元。

大自然真是神奇，不知道AI学界还会给我们带来多少惊喜。

原报告标题：KAN: Language Model for AI+Science

作者：费斌杰（北京市青联委员、熵简科技CEO）